SWAGE
The SWAGE sub-library contains a large suite of mesh data structures, a rich set of index spaces for different geometric entities, and many connectivity arrays between the various index spaces. This library supports both unstructured linear and arbitrary-order meshes. SWAGE is designed to support a diverse range of methods that arise in computational physics and engineering.
A mesh with cubic serendipity elements
SWAGE
The swift Lagrangian to Eulerian (SWAGE) mesh library is very general and allows users to implement a large range of numerical methods on unstructured arbitrary-order 3D meshes. This library supports connectivity data structures and index spaces needed to implement either low-order or high-order numerical methods. SWAGE is designed to work with the elements library that contains e.g., quadrature sets, basis functions, Jacobian matrices, etc. The SWAGE mesh library has unique index spaces to support arbitrary-order Lagrangian material dynamics codes that solve the governing equations for motion on an arbitrary-order mesh that moves with the material. The SWAGE mesh library also allows code developers to create high-order Eulerian fluid dynamics codes using high-order meshes that are conformal to a curved boundary (e.g., a wing). SWAGE relies on the MATAR library to access multidimensional data and couples with the elements library inside the geometry library.
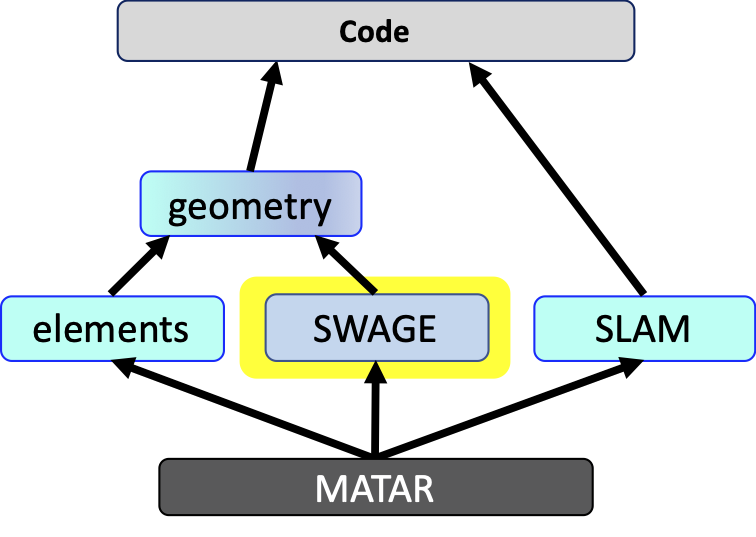
SWAGE code structure
Descriptions
The index spaces in SWAGE are:
elements (the computational mesh is decomposed into non-overlapping elements)
vertices (kinematic degrees of freedom for an element)
nodes (a continuous space that coincides with the Lobatto point locations)
gauss points (a discontinuous space that are the Lobatto point locations)
sub-cells (a decomposition of an element using the nodes), abbreviated as cells
sub-zones (a decomposition of an element using the vertices), abbreviated as zones
surface (a surface of the element)
patch (a portion of the element surface that coincides with the surface of a sub-cell)
facet (a portion of a patch)
corner (a corner of a sub-cell)
Connectivity data structures exist to map from from an index to another index space (e.g., all nodes in an element) and to walk over neighboring mesh entities (e.g., all sub-cells around a sub-cell). The SWAGE library is stitched together with the elements library in the geometry library to support arbitrary-order meshes (i.e., elements with linear or curved edges) and diverse numerical schemes including continuous and discontinuous finite element methods, and finite volume methods.
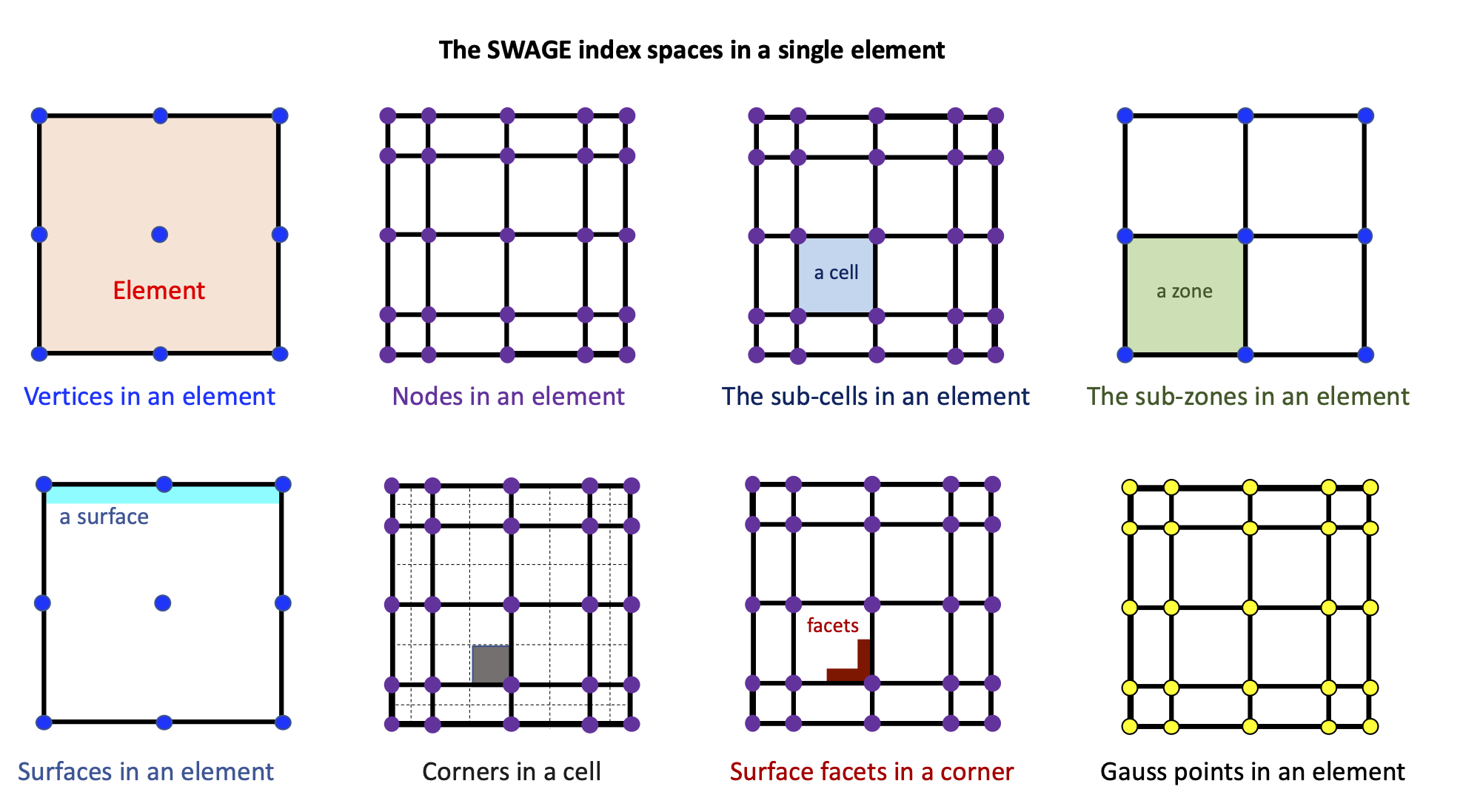
ELEMENTS data structures
Index naming conventions
The global index spaces for the mesh (but local to a rank) are denoted with a gid.
The index spaces for the local mesh entities, relative to a , are denoted with a ``lid.
The index spaces in a reference element, which comes from the elements library and are not in SWAGE, are denoted with a rid.
A local reference index, relative to a rid, is denoted with a rlid.
Connectivity functions naming conventions
The general form of all connectivity structures, in terms an arbitrary mesh entity, is
// entity is generic for illustrative purposes and can be cell, element, node, etc.,
// likewise, something is generic for illustrative purposes and is some mesh entity
for (int something_lid = 0; something_lid < mesh.num_something_in_entity(entity_gid); something_lid++){
int something_gid = mesh.something_in_entity(entity_gid, something_lid);
// ...
}
Usage
To code to walk over all the elements in the mesh and then over all the sub-cells in the element would be
for(int elem_gid = 0; elem_gid < mesh.num_elems(); elem_gid++){
for(int cell_lid = 0; cell_lid < mesh.num_cells_in_elem(); cell_lid++){
int cell_gid = mesh.cells_in_elem(elem_gid, cell_lid); // access the cell mesh index
// ...
}
}
Then, to walk over all the corners in a sub-cell or all the nodes in a sub-cell would be
for(int elem_gid = 0; elem_gid < mesh.num_elems(); elem_gid++){
for(int cell_lid = 0; cell_lid < mesh.num_cells_in_elem(); cell_lid++){
int cell_gid = mesh.cells_in_elem(elem_gid, cell_lid);
for(int node_lid = 0; node_lid < 8; node_lid++){
int node_gid = mesh.nodes_in_cell(cell_gid, node_lid); // access the node mesh index
int corner_gid = mesh.corners_in_cell(cell_gid, node_lid); // access the corner mesh index
// ...
}
}
}
Then, the code to walk over all the surface facets in a corner would be
for(int elem_gid = 0; elem_gid < mesh.num_elems(); elem_gid++){
for(int cell_lid = 0; cell_lid < mesh.num_cells_in_elem(); cell_lid++){
int cell_gid = mesh.cells_in_elem(elem_gid, cell_lid);
for(int node_lid = 0; node_lid < 8; node_lid++){
int node_gid = mesh.nodes_in_cell(cell_gid, node_lid); // access the node mesh index
int corner_gid = mesh.corners_in_cell(cell_gid, node_lid); // access the corner mesh index
for(int facet_lid = 0; facet_lid < 3; facet_lid++){
// ...
}
}
}
}
There are many ways to walk over or access an index space. To just walk over all the nodes in the mesh, the code is
for (int node_gid = 0; node_gid < mesh.num_nodes(); node_gid++) {
// ...
} // end for loop over nodes
Then, to walk over all the corners in a node would be
for (int node_gid = 0; node_gid < mesh.num_nodes(); node_gid++) {
for(int corn_lid = 0; corn_lid < mesh.num_corners_in_node(node_gid); corn_lid++){
int corner_gid = mesh.corners_in_node(node_gid, corn_lid); // access the corner mesh index
// ...
}
} // end for loop over nodes
SWAGE supports unstructured meshes so the number of corners around a node can vary across the mesh. SWAGE offers many ways to access index neighbors. One example is accessing all neighboring cells to a cell
for(int cell_gid = 0; cell_gid < mesh.num_cells(); cell_gid++){
for (int neighbor_lid = 0; neighbor_lid < mesh.num_cells_in_cell(cell_gid); neighbor_lid++){
int neighbor_cell_gid = mesh.cells_in_cell(cell_gid, neighbor_lid); // Get mesh index for the neighboring cell
// ...
}
}
The data structures in SWAGE like mesh.cells_in_cell(cell_gid, neighbor_lid) and mesh.corners_in_node(node_gid, corn_lid) access the data in a contiguous manner to deliver optimal runtime performance.
-
namespace swage
Swage contains a mesh class usefeul for defining geometric entities required for a broad range of numerical methods defined on an nth order hexahedral element.
Functions
-
void lobatto_nodes_1D_tmp(CArray<real_t> &lob_nodes_1D, const int &num)
lobatto_nodes_1D_tmp creates nodal positions defined on [-1,1] using the Gauss-Lobatto quadrature points. This is used in the refine_mesh code to map the new nodal positions from reference space to physical space.
-
class mesh_t
Public Functions
-
void init_element(int e_order, int dim, int num_elem)
mesh_t::init_element takes in the polynomial order used to define the deformation of the element, the dimensionality of the mesh (for now, always 3) and the total number of elements from the mesh that was read in. This information is used to allocate memeory for the geometric entitities local to the element as well as the index maps between them.
-
void init_cells(int ncells)
mesh_t::init_cells takes in the total number of cells necessary for the requested level of refinement. This information is used to allocate memeory for the geometric entitities local to the cell as well as the index maps between them.
-
void init_nodes(int num_nodes)
mesh_t::init_cells takes in the total number of cells necessary for the requested level of refinement. This information is used to allocate memeory for the geometric entitities local to the cell as well as the index maps between them.
-
void init_gauss_pts()
mesh_t::init_gauss_pts allocates memeory for the quadrature points and the geometric entitities associated with them.
-
void init_gauss_patch_pts()
mesh_t::init_gauss_patch_pts allocates memeory for the patch quadrature points and the geometric entitities associated with them. Patch index space must be built first
-
void init_gauss_cell_pts()
mesh_t::init_gauss_cell_pts allocates memeory for the cell quadrature points and the geometric entitities associated with them.
-
void init_bdy_sets(int num_sets)
mesh_t::init_bdy_sets takes in the number of boundary sets and allocates memeory for them as well as the memory required to represent the boundary conditions associated with each set.
-
int num_dim() const
mesh_t::num_dim() returns the dimensionality of the mesh. For now, this should always be 3.
-
int elem_order() const
mesh_t::elem_order() returns the polynomial order used to define the deformation of the element.
-
void init_element(int e_order, int dim, int num_elem)
-
void lobatto_nodes_1D_tmp(CArray<real_t> &lob_nodes_1D, const int &num)