3. Define interior interfaces
Interfaces are defined with the surface command. In this case the boundary type is intrface. If the command defines a volume (e.g. box, cylinder) then the interface is the surface of the volume defined. If the command defines a plane or sheet then the interface is the plane or sheet. It is important to remember that planes are infinite and that the order of points specifying the plane determines a normal to the plane in the usual right-hand-rule sense (see Section II.a.9). This direction is important in determining regions. In order to divide the unit cube defined above in half vertically, define a plane by:
surface/cutplane/intrface /plane/0.,0.,.5/1.,0.,.5/1.,1.,.5
The normal to this plane points in the positive z direction.

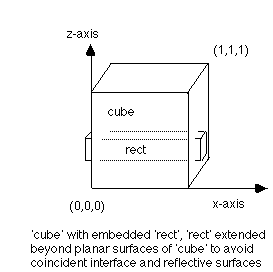
Interfaces must not be coincident with reflective boundaries. For example to embed a rectangle inside a cube, it is necessary to extend the ends of the rectangle beyond the cube to avoid coincident reflective and interface surfaces:
surface/cube/reflect /box/0.0,0.0,0.0/1.0,1.0,1.0
surface/rect /intrface/box/-0.1,0.5,0.2/1.1,0.6,0.5