EOS Models

The mathematical descriptions of these models are presented below while the details of using them is presented in the description of the EOS API.

EOS Theory

An equation of state (EOS) is a constituitive model that generally relates thermodynamic quantities such as pressure, temperature, density, internal energy, free energy, and entropy consistent with the constraints of equillibrium thermodynamics.

singularity-eos contains a number of equations of state that are most useful in hydrodynamics codes. All of the equations of state presented here are considered “complete” equations of state in the sense that they contain all the information needed to derive a given thermodynamic quantity. However, not all variables are exposed since the emphasis is on only those that are needed for hydrodynamics codes. An incomplete equation of state is often sufficient for pure hydrodynamics since it can relate pressure to a given energy-density state, but it is missing thermal information (see the section on complete equations of state).

An excellent resource on equations of state in the context of hydrodynamics is the seminal work from Menikoff and Plohr. In particular, Appendix A contains a number of thermodynamic relationships that can be useful for computing additional quantities from those output in singularity-eos.

The Mie-Gruneisen form

Many of the following equations of state are considered to be of the “Mie-Gruneisen form”, which has many implications but for our purposes means that the general form of the EOS is

\[P - P_\mathrm{ref} = \rho \Gamma(\rho) (e - e_\mathrm{ref})\]

where ‘ref’ denotes quantities along some reference curve, \(P\) is the pressure, \(\rho\) is the density, \(\Gamma\) is the Gruneisen parameter, and \(e\) is the specific internal energy. In this sense, an EOS of this form uses the Gruneisen parameter to describe the pressure behavior of the EOS away from the reference curve. Coupled with a relationship between energy and temperature (sometimes as simple as a constant heat capacity), the complete equation of state can be constructed.

To some degree it is the complexity of the reference state and the heat capacity that will determine an EOS’s ability to capture the complex behavior of a material. At the simplest level, the ideal gas EOS uses a reference state at zero pressure and energy, while more complex equations of state such as the Davis EOS use the material’s isentrope. In ths way, the reference curve indicates the conditions under which you can expect the EOS to represent the intended behavior.

Some Notes on Thermodynamic Consistency

For the pure purpose of solving the Euler equations, an incomplete equation of state of the form \(P(\rho, e)\) is sufficient. In essence, this provides the mechanical response of a material subjected to different types of compression and expansion. However, this EOS is lacking thermal information without an appropriate heat capacity relationship.

As discussed by Mattsson, an equation of state can be considered “complete” if it is constructed from one of the thermodynamic potentials using their natural variables, i.e.

\[\begin{split}e =& e(\rho, S) \\ h =& h(P, S) \\ F =& F(\rho, T) \\ G =& G(P, T) \\\end{split}\]

where all potentials are specific. Here \(e\) is again the internal energy, \(h\) is the enthalpy, \(F\) is the Helmholtz free energy, and \(G\) is the Gibbs free energy. While equations of state formulated using the Helmholtz free energy can be particularly attractive (such as the sesame tables), finding a convenient form can be difficult. As such, it becomes imperitive to extend the Mie-Gruneisen form so that it can form a complete EOS.

The heat capacity is defined as

\[C_V := \left(\frac{\partial e}{\partial T}\right)_V = T \left(\frac{\partial S}{\partial T}\right)_V\]

which provides a natural means by which to relate the entropy/energy to the temperature and form a complete equation of state. However, there are specific requirements placed on the functional form of the heat capacity described below.

The Maxwell relations are the consequence of the requirement that mixed partial second derivatives of the thermodynamic potentials should be independent of the order of differentiation. This concept can be extended to third derivatives (as Davis does in his Appendix B here) to produce the relationship,

\[\frac{V}{C_V^2}\left(\frac{\partial C_V}{\partial V}\right)_S = \left(\frac{\partial \Gamma}{\partial S}\right)_V.\]

This is often referred to as a “compatibility condition” (see also Menikoff) and provides an important connection between the Gruneisen parameter, \(\Gamma\), and the constant volume heat capacity, \(C_V\), in the context of a complete equation of state developed from the internal energy. Importantly, if the Gruneisen form forces us to assume that the Gruneisen parameter is a sole function of density/volume, then the implication is that the heat capacity *must* then be a sole function of entropy.

Again from Menikoff, it can be shown that even in the simplest possible case of a constant heat capacity, the temperature is related to the energy through

\[T(\rho, e) = T_0 \phi(\rho) + \frac{e - e_{S,0}(\rho)}{C_V}\]

where \(T_0\) represents a reference temperature, \(e_{S,0}\) is the energy along the isentrope that passes through the reference temperature, and \(\phi(\rho)\) is an integrating factor given by

\[\phi(\rho) = \exp\left(\int\limits_{\rho_0}^{\rho} \rho \Gamma (\rho) \mathrm{d}\rho \right).\]

As an EOS of a Mie-Gruneisen form becomes more complicated with more complex functional forms for \(\Gamma\) and the reference curves, the task of calculating a thermodynamically consistent temperature becomes more complicated.

Available EOS Information and Nomenclature

The EOS models in singularity-eos are defined for the following sets of dependent and independent variables through various member functions described in the EOS API.

Function	Dependent Variable	Independent Variables
\(T(\rho, e)\)	Temperature	Density, Specific Internal Energy
\(P(\rho, e)\)	Pressure
\(S(\rho, e)\)	Specific Entropy
\(e(\rho, T)\)	Specific Internal Energy	Density, Temperature
\(P(\rho, T)\)	Pressure
\(S(\rho, T)\)	Specific Entropy
\(\rho(P, T)\) [1]	Density	Pressure, [1] Temperature [1]
\(e(P, T)\) [1]	Specific Internal Energy
\(C_V(\rho, T)\)	Constant Volume Specific Heat Capacity	Density, Temperature
\(C_V(\rho, e)\)		Density, Specific Internal Energy
\(B_S(\rho, T)\)	Isentropic Bulk Modulus	Density, Temperature
\(B_S(\rho, e)\)		Density, Specific Internal Energy
\(\Gamma(\rho, T)\)	Gruneisen Parameter	Density, Temperature
\(\Gamma(\rho, e)\)		Density, Specific Internal Energy

[1] (1,2,3,4)

Note: Using pressure and temperature as independent variables is fraught since both pressure and energy are often multi-valued in density for many EOS due to the presence of phase changes (especially tabular EOS). For analytic EOS in singularity-eos where there is not an analytic inversion to pressure-temperature space, a root-find is typically used that uses the density at standard temperature and pressure (STP) as an initial guess. The notable exceptions to this are the spiner EOS that allow the introduction of an initial guess via the lambda function argument.

A point of note is that “specific” implies that the quantity is intensive on a per unit mass basis. It should be assumed that the internal energy and entopry are always specific since we are working in terms of density (the inverse of specific volume).

Entropy availability

For an arbitrary equation of state, a change in entropy in terms of temperature and volume is given by

\[\Delta S = \int\limits_{S_0}^{S} \mathrm{d}S = \int\limits_{T_0}^{T} \left(\frac{\partial S}{\partial T}\right)_V \mathrm{d}T + \int\limits_{V_0}^{V} \left(\frac{\partial S}{\partial V}\right)_T \mathrm{d}V,\]

which can be simplified using a definition of the heat capacity and a Maxwell relation to become

\[\Delta S = \int\limits_{T_0}^{T} \frac{C_V}{T} \mathrm{d}T + \int\limits_{V_0}^{V} \left(\frac{\partial P}{\partial T}\right)_V \mathrm{d}V.\]

Similarly, expressing the entropy in terms of energy and volume yields

\[\Delta S = \int\limits_{e_0}^{e} \frac{1}{T(\rho, e)} \mathrm{d}e + \int\limits_{V_0}^{V} \frac{P(\rho, e)}{T(\rho, e)} \mathrm{d}V\]

after substituting for the appropriate derivatives using the first law of thermodynamics.

Importantly for the analytic EOS, these integrals will tend to diverge as the temperature and volume approach zero if the heat capacity does not also approach zero. This necessitates appropriate choices for the reference states \(T_0\) and \(V_0\).

Note

All EOS objects will expose the functions EntropyFromDensityInternalEnergy () and EntropyFromDensityTemperature() but many EOS cannot currently calculate entropy, either because the EOS is not thermodynamically consistent or because the feature has not yet been implemented. In these cases, the use of these functions will abort the calculation or raise an exception depending on the execution space (host or device). The cases where this occurs are noted below.

Nomenclature Disambiguation

The Gruneisen Parameter

In this description of the EOS models, we use \(\Gamma\) to represent the Gruneisen coeficient since this is the most commonly-used symbol in the context of Mie-Gruneisen equations of state. The definition of the Gruneisen parameter is

\[\Gamma := \frac{1}{\rho} \left( \frac{\partial P}{\partial e} \right)_\rho\]

This should be differentiated from

\[\gamma := \frac{V}{P} \left( \frac{\partial P}{\partial V} \right)_S = \frac{B_S}{P}\]

though, which is the adiabatic exponent.

For an ideal gas, the adiabatic exponent is simply the ratio of the heat capacities,

\[\gamma_\mathrm{id} = \frac{C_P}{C_V} = \frac{B_S}{B_T}.\]

Here \(C_P\) is the specific heat capacity at constant pressure and \(B_T\) is the isothermal bulk modulus.

Units and conversions

The default units for singularity-eos are cgs which results in the following units for thermodynamic quantities:

Quantity	Default Units	cgµ conversion	mm-mg-µs conversion
\(P\)	µbar	10-12 Mbar	10-10 GPa
\(\rho\)	g/cm3	1	1 mg/mm3
\(e\)	erg/g	10-12 Terg/g	10-10 J/mg
\(S\)	erg/g-K	10-12 Terg/g-K	10-10 J/mg-K
\(T\)	K	1	1
\(C_V\)	erg/g/K	10-12 Terg/g/K	10-10 J/mg/K
\(B_S\)	µbar	10-12 Mbar	10-10 GPa
\(\Gamma\)	unitless	–	–

Note: sometimes temperatures are measured in eV for which the conversion is 8.617333262e-05 eV/K.

Sesame units are equivalent to the mm-mg-µs unit system.

Implemented EOS models

Ideal Gas

The ideal gas (aka perfect or gamma-law gas) model in singularity-eos takes the form

\[P = \Gamma \rho e\]

\[e = C_V T,\]

where quantities are defined in the nomenclature section. A common point of confusion is \(\Gamma\) versus \(\gamma\) with the latter being the adiabatic exponent. For an ideal gas, they are related through

\[\Gamma = \gamma - 1\]

Although this formulation differs from the traditional representation of the ideal gas law as \(P\tilde{V} = RT\), the forms are equivalent by recognizing that \(\Gamma = \frac{R}{\tilde{C_V}}\) where \(R\) is the ideal gas constant in units of energy per mole per Kelvin and \(\tilde {C_\mathrm{V}}\) is the molar heat capacity, relatable to the specific heat capacity through the molecular weight of the gas. Since \(\tilde{C_\mathrm {V}} = \frac{5}{2} R\) for a diatomic ideal gas, the corresponding Gruneisen parameter should be 0.4.

The entropy for an ideal gas is given by

\[S = C_V \ln\left(\frac{T}{T_0}\right) + \Gamma C_V \ln\left(\frac{\rho_0} {\rho}\right),\]

Note

The entropy diverges to negative infinity at absolute zero due to the constant heat capacity assumption. Care should be taken when using temperatures significantly below that of the reference state.

we have assumed that the entropy is zero at the reference state given by \(T_0\) and \(\rho_0\). By default, \(T_0 = 298\) K and the reference density is given by

\[\rho_0 = \frac{P_0}{\Gamma C_V T_0},\]

where \(P_0 = 1\) bar.

It should be noted that this equation diverges as the temperature approaches zero or the density approaches infinity. From a physical perspective, this is a limitation of the constant heat capacity assumption and would be remedied if the heat capacity went to zero at absolute zero. However, this represents a significant deviation from true ideal gas physics so we do not include it here.

The settable parameters for this EOS are the Gruneisen parameter and specific heat capacity. Optionally, the reference state for the entropy calculation can be provided by setting both the reference density and temperature.

The IdealGas EOS constructor has two arguments, gm1, which is the Gruneisen parameter \(\Gamma\), and Cv, which is the specific heat \(C_V\):

IdealGas(Real gm1, Real Cv)

Optionally, the reference temperature and density for the entropy calculation, can be provided in the constructor via EntropyT0 and EntropyRho0:

IdealGas(Real gm1, Real Cv, Real EntropyT0, Real EntropyRho0)

Note that these parameters are provided solely for the entropy calculation. When these values are not set, they will be the same as those returned by the ValuesAtReferenceState() function. However, if the entropy reference conditions are given, the return values of the ValuesAtReferenceState() function will not be the same.

Stiffened Gas

The following implementation was guided by the reference StiffGas. The stiffened gas model in singularity-eos takes the form

\[P = \Gamma \rho (e-q) - \gamma P_{\infty}\]

\[e = \frac{ P + \gamma P_{\infty} }{ P + P_{\infty} } C_V T + q,\]

where quantities are largely the same as ideal gas with the exception of \(P_{\infty}\) and \(q\), which can be thought of as an offset pressure and internal energy, respectively.

The entropy for a stiffened gas can be expressed as

\[S = C_V \ln\left(\frac{T}{T_0}\right) + (\gamma-1) C_V \ln\left(\frac{\rho_0} {\rho}\right) + q',\]

where \(S(\rho_0,T_0)=q'\). By default, \(T_0 = 298\) K and the reference density is given by

\[\rho_0 = \frac{P_0 + P_{\infty}}{(\gamma-1) C_V T_0},\]

where the reference pressure, \(P_0\), is 1 bar by default.

The settable parameters for this EOS are the Gruneisen parameter, \(\gamma-1\), specific heat capacity, \(C_V\), offset pressure, \(P_{\infty}\), and the offset internal energy, \(q\). Optionally, the reference state for the entropy calculation can be provided by setting values for the reference temperature, pressure, and offset entropy (\(q'\)).

The StiffGas EOS constructor has four arguments, gm1, which is the Gruneisen parameter \(\Gamma\), Cv, which is the specific heat \(C_V\), P_{\infty} which is the offset pressure, and q which is the offset internal energy:

StiffGas(Real gm1, Real Cv, Real Pinf, Real q)

Optionally, the reference temperature and density for the entropy calculation, can be provided in the constructor via qp, T0, and P0:

StiffGas(Real gm1, Real Cv, Real Pinf, Real q, Real qp, Real T0, Real P0)

Note that these parameters are provided solely for the entropy calculation. When these values are not set, they will be the same as those returned by the ValuesAtReferenceState() function. However, if the entropy reference conditions are given, the return values of the ValuesAtReferenceState() function will not be the same.

Noble-Abel

The implementation here was influenced by the reference NobleAbel. The Noble-Abel (aka Clausius I or Hirn) model in singularity-eos takes the form

\[P = \frac{ \rho (e-q) (\gamma-1) }{ 1 - b \rho }\]

\[e = C_V T + q,\]

where quantities are similar to the ideal gas law with the exception of covolume (\(b\)) and offset internal energy (\(q\)). It should be noted that covolume is physically significant as it represents the maximum compressibility of the gas, and as a result it should be non-negative.

The entropy for the Noble-Abel EoS is given by

\[S = C_V \ln\left(\frac{T}{T_0}\right) + C_V (\gamma-1) \ln\left(\frac{v - b} {v_0 - b}\right) + q',\]

where \(S(\rho_0,T_0)=q'\). By default, \(T_0 = 298\) K and the reference density is given by

\[\rho_0 = \frac{P_0}{C_V T_0(\gamma-1) + bP_0},\]

where \(P_0\) is by default 1 bar.

The settable parameters for this EOS are \(\gamma-1\), specific heat capacity (\(C_V\)), covolume (\(b\)) and offset internal energy (\(q\)). Optionally, the reference state for the entropy calculation can be provided by setting the reference temperature, pressure, and entropy offset.

The NobleAbel EOS constructor has four arguments: gm1, which is \(\gamma-1\); Cv, the specific heat \(C_V\); \(b\), the covolume; and \(q\), the internal energy offset.

NobleAbel(Real gm1, Real Cv, Real b, Real q)

Optionally, the reference state for the entropy calculation, can be provided in the constructor via qp, T0 and P0:

NobleAbel(Real gm1, Real Cv, Real b, Real q, Real qp, Real T0, Real P0)

Note that these parameters are provided solely for the entropy calculation. When these values are not set, they will be the same as those returned by the ValuesAtReferenceState() function. However, if the entropy reference conditions are given, the return values of the ValuesAtReferenceState() function will not be the same.

Carnahan-Starling

The (quasi-exact) Carnahan-Starling model in singularity-eos takes the form

\[P = Z(\rho) \rho (e-q) (\gamma-1)\]

\[Z(\rho) = \frac{1+\eta+\eta^2-\eta^3}{(1-\eta)^3},\]

where \(\eta\) is the packing fraction given by

\[\eta = b\rho.\]

The energy is related to the temperature through

\[e = C_V T + q,\]

where \(q\) is an energy offset.

As with the Noble-Abel EOS, it should be noted that covolume is physically significant as it represents the maximum compressibility of the gas, and as a result it should be non-negative.

The Carnahan-Starling EOS is intended to represent a hard sphere fluid, and the covolume parameter, \(b\), can be related to the hard sphere diameter, \(\sigma\), through

\[b = \frac{\pi}{6}\frac{\sigma^3}{M},\]

where \(M\) is the molar mass of the gas.

The entropy for the Carnahan-Starling EOS is given by

\[S = C_V \ln\left(\frac{T}{T_0}\right) + C_V (\gamma-1) \left\{ \ln\left(\frac{v} {v_0}\right) - S^{CS} \right\} + q',\]

\[S^{CS} = b\left(4\left(\frac{1}{v-b} - \frac{1}{v_0-b}\right)+ b\left(\frac{1}{(v-b)^2} - \frac{1}{(v_0-b)^2}\right)\right)\]

where \(S(\rho_0,T_0)=q'\). By default, \(T_0 = 298\) K and the reference density is given by

\[P_0 = \rho_0 Z(\rho_0) C_V T_0(\gamma-1),\]

where \(P_0\) is by default 1 bar. Denisty is obtained through root finding methods.

The settable parameters for this EOS are \(\gamma-1\), specific heat capacity (\(C_V\)), covolume (\(b\)) and offset internal energy (\(q\)). Optionally, the reference state for the entropy calculation can be provided by setting the reference temperature, pressure, and entropy offset.

The CarnahanStarling EOS constructor has four arguments: gm1, which is \(\gamma-1\); Cv, the specific heat \(C_V\); \(b\), the covolume; and \(q\), the internal energy offset.

CarnahanStarling(Real gm1, Real Cv, Real b, Real q)

Optionally, the reference state for the entropy calculation, can be provided in the constructor via qp, T0 and P0:

CarnahanStarling(Real gm1, Real Cv, Real b, Real q, Real qp, Real T0, Real P0)

Note that these parameters are provided solely for the entropy calculation. When these values are not set, they will be the same as those returned by the ValuesAtReferenceState() function. However, if the entropy reference conditions are given, the return values of the ValuesAtReferenceState() function will not be the same.

Gruneisen EOS

Warning

Entropy is not available for this EOS

One of the most commonly-used EOS to represent solids is the Steinberg variation of the Mie-Gruneisen EOS, often just shortened to “Gruneisen” EOS. This EOS uses the Hugoniot as the reference curve and thus is extremly powerful because the basic shock response of a material can be modeled using minimal parameters.

The pressure follows the traditional Mie-Gruneisen form,

\[P(\rho, e) = P_H(\rho) + \rho\Gamma(\rho) \left(e - e_H(\rho) \right),\]

Here the subscript \(H\) is a reminder that the reference curve is a Hugoniot. Other quantities are defined in the nomenclature section.

The above is an incomplete equation of state because it only relates the pressure to the density and energy, the minimum required in a solution to the Euler equations. To complete the EOS and determine the temperature, a constant heat capacity is assumed so that

\[T(\rho, e) = \frac{e}{C_V} + T_0\]

The user should note that this implies that \(e=0\) at the reference temperature, \(T_0\). Given this simple relationship, the user should treat the temperature from this EOS as only a rough estimate.

Given the inconsisetency in the temperature, we have made the choice not to expose the entropy for this EOS. Requesting an entropy value will result in an error.

If a linear \(U_s\)-\(u_p\) relation is enough for your problem, we recommend using the MGUsup EOS described below. It is a complete EOS with consistent temperature.

Given a reference density, \(\rho_0\), we first parameterize the EOS using \(\eta\) as a measure of compression given by

\[\eta = 1 - \frac{\rho_0}{\rho}.\]

This is convenient because \(eta = 0\) when \(\rho = \rho_0\), \(\eta = 1\) at the infinite density limit, and \(\eta = -\infty\) at the zero density limit. The Gruneisen parameter, \(\Gamma\) can be expressed in terms of \(\eta\) as

\[\begin{split}\Gamma(\rho) = \begin{cases} \Gamma_0 & \eta \leq 0 \\ \Gamma_0 (1 - \eta) + b\eta & 0 \leq \eta < 1 \end{cases}\end{split}\]

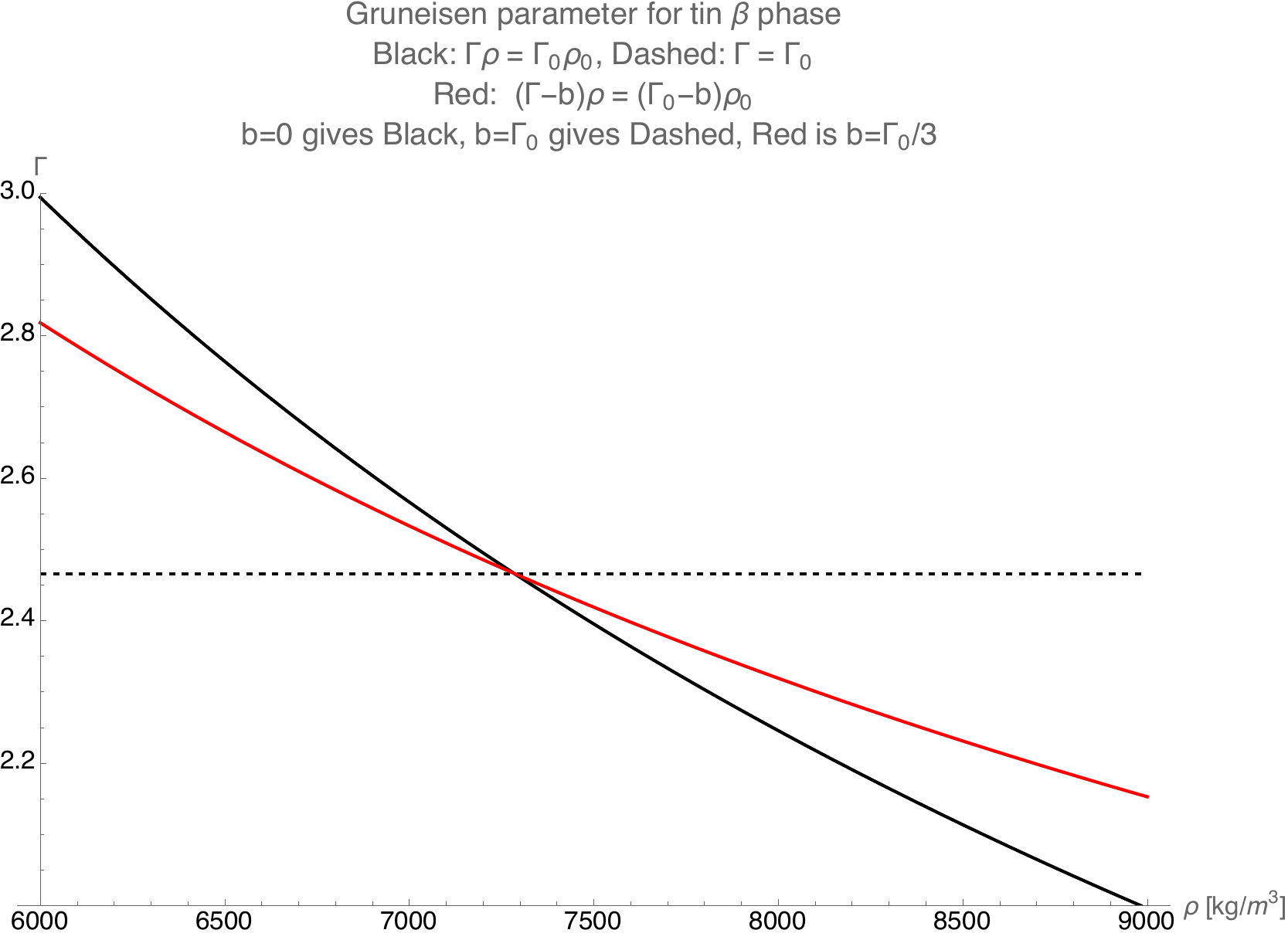
When the unitless user parameter \(b=0\), the Gruneisen parameter is of a form where \(\rho\Gamma =\) constant in compression, i.e. when \(\eta > 0\). If the unitless user parameter \(b=\Gamma_0\), the Gruneisen parameter is of a form where \(\Gamma_0 =\) constant in compression. These two limitig cases are shown in the figure below.

The reference pressure along the Hugoniot is determined by

\[\begin{split}P_H(\rho) = P_0 + c_0^2 \eta \begin{cases} \rho & \rho < \rho_0 \\ \frac{\rho_0}{\left( 1 - s_1 \eta - s_2 \eta^2 - s_3 \eta^3 \right)^2} & \rho \geq \rho_0 \end{cases}\end{split}\]

where \(P_0\) is the reference pressure and \(c_0\), \(s_1\), \(s_2\), and \(s_3\) are fitting paramters to the \(U_s\)-\(u_p\) curve such that

\[U_s = c_0 + u_p \left( s_1 + s_2 \frac{u_p}{U_s} + s_3\left(\frac{u_p}{U_s}\right)^2 \right).\]

Here \(U_s\) is the shock velocity and \(u_p\) is the particle velocity. For many materials, this relationship is roughly linear so only the \(s_1\) parameter is needed. The units for \(c_0\) are velocity while the rest are unitless. Note that the parameter \(s_1\) is related to the fundamental derivative of shock physics as shown by Wills.

Finally the energy along the Hugoniot is given by

\[\begin{split}E_H(\rho) = \begin{cases} 0 & \rho < \rho_0 \\ \frac{\eta (P_H + P_0)}{2 \rho_0} & \rho \geq \rho_0 \end{cases}.\end{split}\]

One should note that in this form neither the expansion region nor the overall temperature are thermodynamically consistent with the rest of the EOS. Since the EOS is a fit to the principal Hugoniot, the EOS will obviously reproduce single shocks quite well, but it may not be as appropriate when there are multiple shocks or for modeling the release behavior of a material.

The constructor for the Gruneisen EOS has the signature

Gruneisen(const Real C0, const Real s1, const Real s2, const Real s3, const Real G0,
          const Real b, const Real rho0, const Real T0, const Real P0, const Real Cv,
          const Real rho_max)

where C0 is \(C_0\), s1 is \(s_1\), s2 is \(s_2\), s3 is \(s_3\), G0 is \(\Gamma_0\), b is \(b\), rho0 is \(\rho_0\), T0 is \(T_0\), P0 is \(P_0\), and Cv is \(C_v\). rho_max is the maximum value of density for which the reference pressure curve is valid. Input densities above rho_max are pinned to rho_max.

There is an overload of the Gruneisen class which computes rho_max automatically without the user needing to specify:

Gruneisen(const Real C0, const Real s1, const Real s2, const Real s3, const Real G0,
          const Real b, const Real rho0, const Real T0, const Real P0, const Real Cv)

Extendended Vinet EOS

The extended Vinet EOS is a full EOS, extended in both temperature and density from the Vinet universal EOS for solids (also called Rose cold curve). It is expected to work well in compression but is untested in expansion. It is published in Appendix 2 in J. Appl. Phys. 119, 015904 (2016).

While the Mie-Gruneisen EOS is based on a Hugoniot as reference curve, the Vinet is based on an isotherm:

\[P(\rho,T) = P_{ref}(\rho) + \alpha_0 B_0 (T - T_{ref})\]

where the reference isotherm is

\[\begin{split}P_{ref}(X)&=\frac{3 B_0}{X^2} Z \exp[\eta_0 Z] \left( 1 + \sum_{n=2}^N d_n Z^n \right) \, , \\ X &= \left( \frac{\rho_0}{\rho} \right)^{1/3} \\ Z &= 1-X\end{split}\]

Note that \(P_{ref}=0\) when \(\rho = \rho_0\), the reference state on the reference isotherm is always at ambient pressure. However, the reference isotherm is not necessarily at room temperature.

It can be shown that \(B_0\) is the isothermal bulk modulus, and \(\alpha_0\) the thermal expansion coefficient, at the reference state, and that

\[\eta_0 = \frac{3}{2}\left[ \left[ \frac{\partial B}{\partial P}\right]_0 -1\right] \, .\]

By assuming that also the constant volume heat capacity is a constant, \({C_V}_0\), an entropy can be derived

\[S(V,T) = S_0 + \alpha_0 B_0 (V - V_0) + {C_V}_0 \ln \frac{T}{T_{ref}}\]

and from that a thermodynamic consistent energy

\[\begin{split}E(X,T) =& 9 \frac{B_0 V_0}{{\eta_0}^2}\left(f_0 - \exp[\eta_0 Z] \left (f_0 - \eta_0 Z \left(f_0 + \sum_{n=1}^N f_n Z^n \right)\right)\right) \\ & - \alpha_0 B_0 V_0 (1-X^3) T_{ref} + {C_V}_0 (T - T_{ref}) + E_0\end{split}\]

where the energy coefficients \(f_n\) are determined from the pressure coefficients \(d_n\), \(n\geq 2\), by

\[\begin{split}f_N &= d_N \\ f_n &= d_n - \frac{n+2}{\eta_0} f_{n+1} \\ d_0 &= 1.0 \\ d_1 &= 0.0\end{split}\]

Note

The entropy diverges to negative infinity at absolute zero due to the constant heat capacity assumption. Care should be taken when using temperatures significantly below that of the reference state.

The constructor for the Vinet EOS has the signature

Vinet(const Real rho0, const Real T0, const Real B0, const Real BP0, const Real A0,
           const Real Cv0, const Real E0, const Real S0, const Real *expconsts)

where rho0 is \(\rho_0\), T0 is \(T_{ref}\), B0 is \(B_0\), BP0 is \((\partial B/\partial P)_0\), A0 is \(\alpha_0\), Cv0 is \({C_V}_0\), E0 is \(E_0\), S0 is \(S_0\), and expconsts is a pointer to the constant array of length 39 containing the expansion coefficients \(d_2\) to \(d_{40}\). Expansion coefficients not used should be set to 0.0.

Mie-Gruneisen linear \(U_s\)- \(u_p\) EOS

One of the most commonly-used EOS is the linear \(U_s\)- \(u_p\) version of the Mie-Gruneisen EOS. This EOS uses the Hugoniot as the reference curve and is extensively used in shock physics. This version implements the exact thermodynamic temperature on the Hugoniot and also adds an entropy.

The pressure follows the traditional Mie-Gruneisen form,

\[P(\rho, e) = P_H(\rho) + \rho\Gamma(\rho) \left(e - e_H(\rho) \right),\]

Here the subscript \(H\) is a reminder that the reference curve is a Hugoniot. \(\Gamma\) is the Gruneisen parameter and the first approximation is that \(\rho\Gamma(\rho)=\rho_0\Gamma(\rho_0)\) which is the same assumption as in the Gruneisen EOS when \(b=0\).

The above is an incomplete equation of state because it only relates the pressure to the density and energy, the minimum required in a solution to the Euler equations. To complete the EOS and determine the temperature and entropy, a constant heat capacity is assumed so that

\[T(\rho, e) = \frac{\left(e-e_H(\rho)\right)}{C_V} + T_H(\rho)\]

Note the difference from the Gruneisen EOS described above. We still use a constant \(C_V\), and it is usually taken at the reference temperature, but we now extrapolate from the temperature on the Hugoniot, \(T_H(\rho)\), and not from the reference temperature, \(T_0\).

With this consistent temperature we can derive an entropy in a similar way as for the Vinet EOS. Using thermodynamic derivatives we can show that

\[\Gamma \rho = \frac{\alpha B_T}{C_V} ,\]

and we arrive at

\[S(\rho,T) = S_0 - \Gamma(\rho_0)C_V \eta + {C_V} \ln \frac{T}{T_0} ,\]

where \(\eta\) is a measure of compression given by

\[\eta = 1 - \frac{\rho_0}{\rho}.\]

This is convenient because \(\eta = 0\) when \(\rho = \rho_0\), \(\eta = 1\) at the infinite density limit, and \(\eta = -\infty\) at the zero density limit.

The pressure, energy, and temperature, on the Hugoniot are derived from the shock jump conditions,

\[\begin{split}\rho_0 U_s &= \rho (U_s - u_p) \\ P_H &= \rho_0 U_s u_p \ ,\end{split}\]

assuming a linear \(U_s\)- \(u_p\) relation,

\[U_s = C_s + s u_p .\]

Here \(U_s\) is the shock velocity and \(u_p\) is the particle velocity. As is pointed out in the description of the Gruneisen EOS, for many materials, the \(U_s\)- \(u_p\) relationship is roughly linear so only this \(s\) parameter is needed. The units for \(C_s\) is velocity while \(s\) is unitless. Note that the parameter \(s\) is related to the fundamental derivative of shock physics as shown by Mattsson-Wills.

Solving the jump equations above gives that the reference pressure along the Hugoniot is determined by

\[P_H(\rho) = C_s^2 \rho_0 \frac{\eta}{\left(1 - s \eta \right)^2} .\]

Note the singularity at \(s \eta = 1\) which limits this model’s validity to compressions \(\eta << 1/s\). If your problem can be expected to have compressions of this order, you should use the PowerMG EOS that is explicitely constructed for large compressions. The assumption of linear \(U_s\)- \(u_p\) relation is simply not valid at large compressions.

The energy along the Hugoniot is given by

\[E_H(\rho) = \frac{P_H \eta }{2 \rho_0} + E_0 .\]

The temperature on the Hugoniot is hard to derive explicitely but with the help of Mathematica we can solve

(1)\[T_H(\rho) = T_0 e^{\Gamma(\rho_0) \eta} + \frac{e^{\Gamma(\rho_0) \eta}}{2 C_V \rho_0} \int_0^\eta e^{-\Gamma(\rho_0) z} z^2 \frac{d}{dz} \left( \frac{P_H}{z}\right) dz\]

into the explicit formula

\[\begin{split}T_H(\rho) &= T_0 e^{\Gamma(\rho_0) \eta} + \frac{C_s^2}{2 C_V s^2} \left[\frac{- s \eta}{(1 - s \eta)^2} + \left( \frac{\Gamma(\rho_0)}{s} - 3 \right) \left( e^{\Gamma(\rho_0) \eta} - \frac{1}{(1-s \eta)}\right)\right. \\ & \ \left. + e^{-\frac{\Gamma(\rho_0)}{s} (1-s \eta)} \left( Ei(\frac{\Gamma(\rho_0)}{s}(1-s \eta))-Ei(\frac{\Gamma(\rho_0)}{s}) \right) \left((\frac{\Gamma(\rho_0)}{s})^2 - 4 \frac{\Gamma(\rho_0)}{s} + 2 \right) \right]\end{split}\]

where \(Ei\) is the exponential integral function. We replace the \(Ei\) difference with a sum with cutoff giving an error less than machine precision. For \(s \eta\) close to \(0\), there are severe cancellations in this formula and we use the expansion

\[{T_H}_{exp}(\rho) = T_0 e^{\Gamma(\rho_0) \eta} + \frac{C_s^2}{2 C_V s^2} \left[ -2 \ln ( 1- s \eta) + \frac{s \eta}{(1 - s \eta)^2} ( 3 s \eta - 2) \right] \ .\]

The first omitted term in the expansion inside the square brackets is \(\Gamma(\rho_0) \eta^4 / 6\). This expansion is in fact even better than the common approximation of replacing the full temperature on the Hugoniot with the temperature on the isentrope, that is, the first term \(T_0 e^{\Gamma(\rho_0) \eta}\).

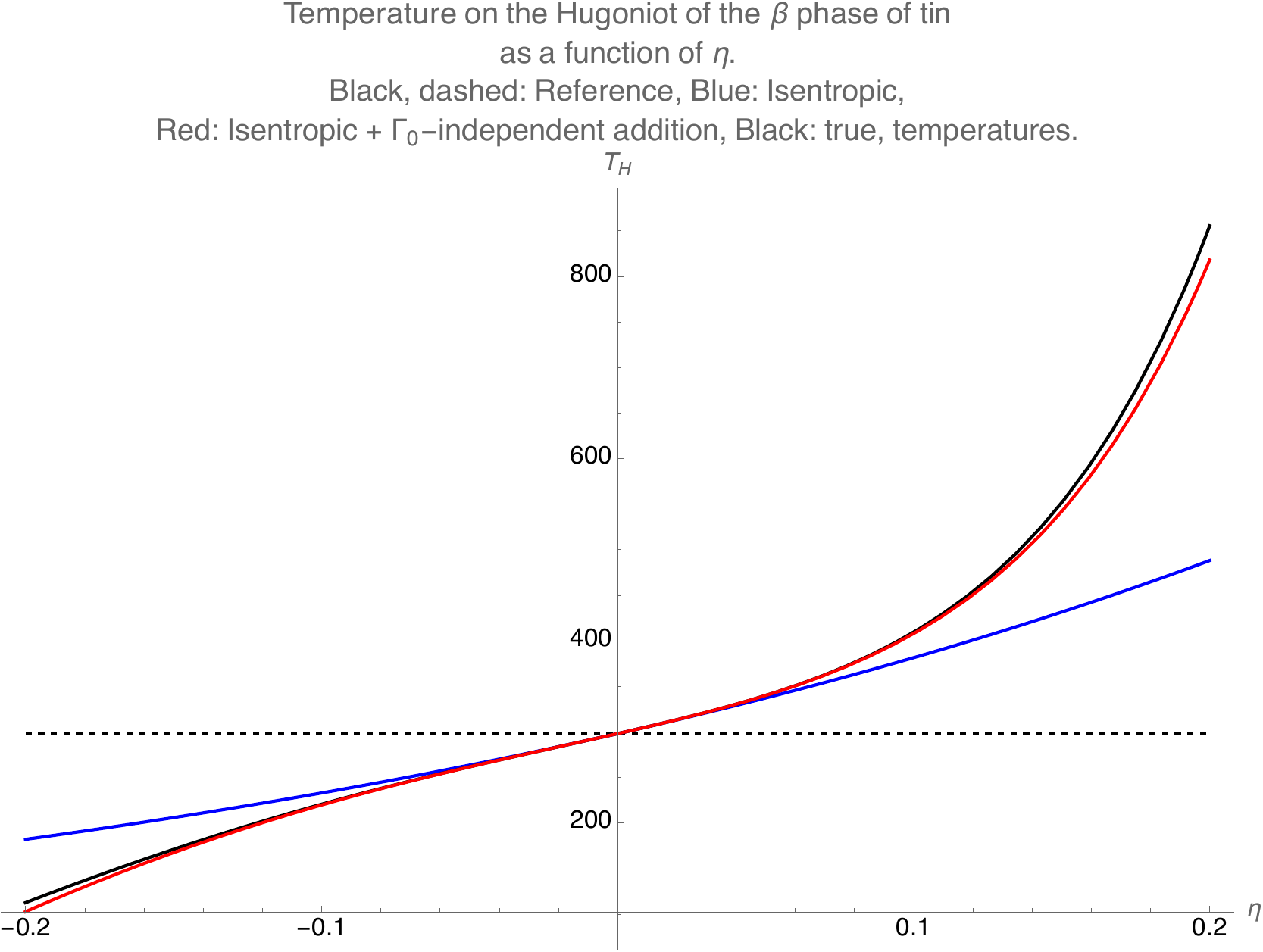
The constructor for the MGUsup EOS has the signature

MGUsup(const Real rho0, const Real T0, const Real Cs, const Real s, const Real G0,
       const Real Cv0, const Real E0, const Real S0)

where rho0 is \(\rho_0\), T0 is \(T_0\), Cs is \(C_s\), s is \(s\), G0 is \(\Gamma(\rho_0)\), Cv0 is \(C_V\), E0 is \(E_0\), and S0 is \(S_0\).

Mie-Gruneisen power expansion EOS

As we noted above, the assumption of a linear \(U_s\)- \(u_p\) relation is simply not valid at large compressions. At Sandia National Laboratories Z-pinch machine, the compression is routinely so large that a new Mie-Gruneisen EOS was developped, by Robinson, that could handle these large compressions. The overall structure and motivation for approximations are as described above; in compression it is only the formula for \(P_H\), and by extension \(T_H\), that differ. This EOS is however modified in expansion to follow an isentrope instead of the invalid-in-expansion Hugoniot.

In the PowerMG model the pressure on the Hugoniot in the compression region, \(\eta \geq 0\) is expressed as a power series

\[P_H(\rho) = K_0 \eta \left( 1 + K_1 \eta + K_2 \eta^2 + K_3 \eta^3 + \cdots + K_M \eta^M \right)\]

By expanding the MGUsup Hugoniot pressure into a power series in \(\eta\) we see that we can recover the MGUsup results by setting

\[\begin{split}K_0 &=& C_s^2 \rho_0 \ \ \ \ \ \ \ \ & \\ K_n &=& (n+1) s^n & \ \ \ \ \ \ n >= 1\end{split}\]

In the figure below we have used \(M=20\) with these coefficients and show how the divergence in the MGUsup pressure at \(\eta = \frac{1}{s}\) is avoided in the PowerMG, making it more suitable for modeling high pressures.

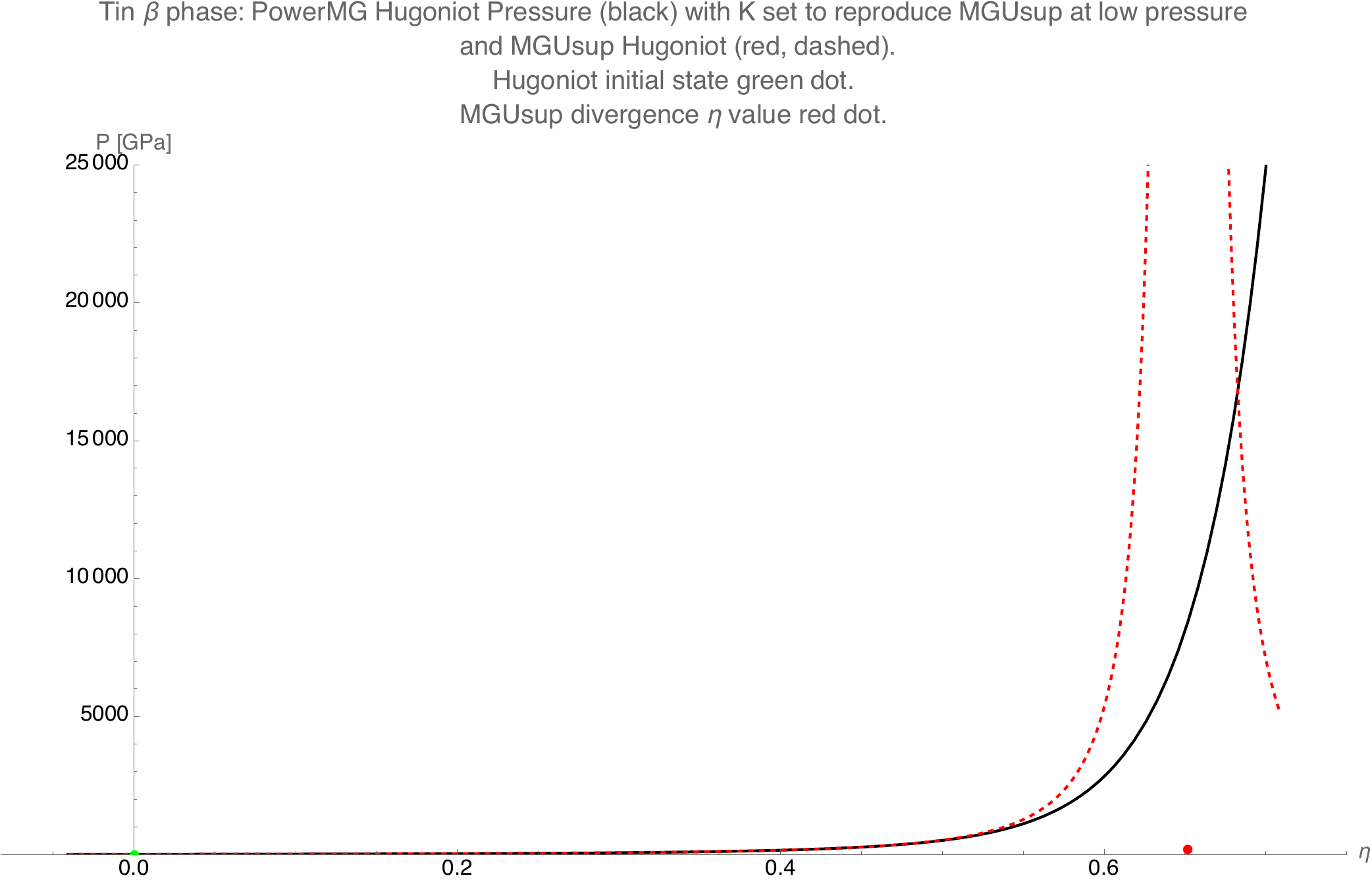
For \(\eta < 0\), that is, in expansion, the isentrope with a single \(K_0\) is used until a user defined minimum pressure is obtained

\[\begin{split}P_H &= K_0 \eta& \ \ \ \ \ \ \ \ \ \ & \frac{P_{min}}{K_0} \leq \eta < 0 \\ P_H &= P_{min} & \ \ \ \ \ \ \ \ \ \ & \eta < \frac{P_{min}}{K_0}\end{split}\]

If the user have not set \(P_{min}\) or if a positive value has been given, a default value of \(P_{min} = -1000 K_0\) is used.

If we now insert the formula for \(P_H\) in compression into equation (1), for \(\eta \geq 0\) we arrive at

\[T_H = T_0 e^{\Gamma(\rho_0) \eta} + \frac{e^{\Gamma(\rho_0) \eta}}{2 C_V \rho_0} K_0 \left( K_1 I_2 + 2 K_2 I_3 + 3 K_3 I_4 + \cdots + M K_M I_{M+1} \right)\]

where

\[I_n = \int_0^\eta e^{-\Gamma(\rho_0) z} z^{n-1} dz\]

that can be rewritten in terms of the lower incomplete gamma function. For \(\eta < 0\) the isentropic temperature is used,

\[T_H = T_0 e^{\Gamma(\rho_0) \eta} \ \ \ \ \ \ \ \ \ \ \eta < 0 \, .\]

It has been verified that this temperature is following the black, true temperature line in the figure late in the MGUsup section in compression and the blue isentropic temperature in expansion. More information about how to implement \(T_H\) into codes is given in Robinson.

For completeness we give \(E_H\) as well,

\[\begin{split}E_H &= \frac{P_H \eta}{2 \rho_0} + E_0 & \ \ \ \ \ \ \ \ \ \ & \eta \geq 0 \\ E_H &= \frac{K_0 \eta^2}{2 \rho_0} + E_0 & \ \ \ \ \ \ \ \ \ \ & \frac{P_{min}}{K_0} \leq \eta < 0 \\ E_H &= \frac{K_0 \eta_{min}^2}{2 \rho_0} + E_0 + \frac{P_{min}}{\rho_0} (\eta - \eta_{min})& \ \ \ \ \ \ \ \ \ \ & \eta < \eta_{min} = \frac{P_{min}}{K_0}\end{split}\]

The constructor for the PowerMG EOS has the signature

PowerMG(const Real rho0, const Real T0, const Real G0, const Real Cv0, const Real E0,
        const Real S0, const Real Pmin, const Real *expconsts)

where rho0 is \(\rho_0\), T0 is \(T_0\), G0 is \(\Gamma(\rho_0)\), Cv0 is \(C_V\), E0 is \(E_0\), S0 is \(S_0\), Pmin is \(P_{min}\), and expconsts is a pointer to the constant array of length 41 containing the expansion coefficients \(K_0\) to \(K_{40}\). Expansion coefficients not used should be set to \(0.0\).

JWL EOS

Warning

Entropy is not available for this EOS

The Jones-Wilkins-Lee (JWL) EOS is used mainly for detonation products of high explosives. Similar to the other EOS here, the JWL EOS can be written in a Mie-Gruneisen form as

\[P(\rho, e) = P_S(\rho) + \rho w (e - e_S(\rho))\]

where the reference curve is an isentrope of the form

\[P_S(\rho) = A \mathrm{e}^{-R_1 \eta} + B \mathrm{e}^{-R_2 \eta}\]

\[e_S(\rho) = \frac{A}{\rho_0 R_1} \mathrm{e}^{-R_1 \eta} + \frac{B}{\rho_0 R_2} \mathrm{e}^{-R_2 \eta}.\]

Here \(\eta = \frac{\rho_0}{\rho}\) and \(R_1\), \(R_2\), \(A\), \(B\), and \(w\) are constants particular to the material. Note that the parameter \(w\) is simply the Gruneisen parameter and is assumed constant for the EOS (which is fairly reasonable since the detonation products are gasses).

Finally, to complete the EOS the energy is related to the temperature by

\[e = e_S(\rho) + C_V T\]

where \(C_V\) is the constant volume specific heat capacity.

The constructor for the JWL EOS is

JWL(const Real A, const Real B, const Real R1, const Real R2,
    const Real w, const Real rho0, const Real Cv)

where A is \(A\), B is \(B\), R1 is \(R_1\), R2 is \(R_2\), w is \(w\), rho0 is \(\rho_0\), and Cv is \(C_V\).

Davis EOS

The Davis reactants and products EOS are both of Mie-Gruneisen forms that use isentropes for the reference curves. The equations of state are typically used to represent high explosives and their detonation products and the reference curves are calibrated to several sets of experimental data.

For both the reactants and products EOS, the pressure and energy take the forms

\[P(\rho, e) = P_S(\rho) + \rho\Gamma(\rho) \left(e - e_S(\rho) \right)\]

\[e(\rho, P) = e_S(\rho) + \frac{1}{\rho \Gamma(\rho)} \left(P - P_S(\rho) \right),\]

where the subscript \(S\) denotes quantities along the reference isentrope and other quantities are defined in the nomenclature section.

Davis Reactants EOS

Warning

Entropy is not yet available for this EOS

The Davis reactants EOS uses an isentrope passing through a reference state and as the reference curve and then assumes that the heat capacity varies linearly with entropy such that

\[C_V = C_{V,0} + \alpha(S - S_0),\]

where subscript \(0\) refers to the reference state and \(\alpha\) is a dimensionless constant specified by the user.

The Gruneisen parameter is given a linear form such that

\[\begin{split}\Gamma(\rho) = \Gamma_0 + \begin{cases} 0 & \rho < \rho_0 \\ Zy & \rho >= \rho_0 \end{cases}\end{split}\]

where \(Z\) is a dimensionless parameter and \(y = 1 - \rho0/\rho\). Along an isentrope, the Gruneisen parameter can be expressed as

\[\Gamma_S(\rho) = \frac{\rho}{T} \left(\frac{\partial T}{\partial \rho}\right)_S,\]

which, upon integration can produce the temperature along the reference isentrope:

\[\begin{split}T_{S,0}(\rho) = \begin{cases} T_0\left(\frac{\rho}{\rho_0}\right)^{\Gamma_0} & \rho < \rho_0 \\ T_0\exp\left(-Zy\right)\left(\frac{\rho}{\rho_0}\right)^{\Gamma_0 + Z} & \rho >= \rho_0 \end{cases}\end{split}\]

where \(T_{S,0}\) is the temperature along the reference isentrope, \(S = S_0\).

Using the fact that the heat capacity can be expressed as

\[C_V = T\left( \frac{\partial S}{\partial T} \right)_V,\]

the temperature off of the reference isoentrope can be integrated from this identity to yield

\[T(\rho, S) = T_{S,0}(\rho) \left( \frac{C_V(S)}{C_{V,0}} \right)^{\frac{1}{\alpha}},\]

Now requiring that the entropy go to zero at absolute zero in accordance with the Nernst postulate and the third law of thermodynamics, the entropy can be expressed as a function of temperature and density such that

\[S(\rho, T) = \frac{C_{V,0}}{\alpha} \left( \frac{T}{T_{S,0}(\rho)} \right)^\alpha.\]

The \(e(\rho, P)\) formulation can now be more-conveniently cast in terms of termperature such that

\[e(\rho, T) = e_S(\rho) + \frac{C_{V,0} T_S(\rho)}{1 + \alpha} \left( \left(\frac{T}{T_S(\rho)} \right)^{1 + \alpha} - 1 \right),\]

which can easily be inverted to find \(T(\rho, e)\).

Finally, the pressure and energy along the isentrope are given by

\[\begin{split}P_S(\rho) = P_0 + \frac{\rho_0 A^2}{4B} \begin{cases} \exp \left( 4By \right) -1 & \rho < \rho_0 \\ \sum\limits_{j=1}^3 \frac{(4By)^j}{j!} + C\frac{(4By)^4}{4!} + \frac{y^2}{(1-y)^4} & \rho >= \rho0 \end{cases}\end{split}\]

\[e_S(\rho) = e_0 + \int\limits_{\rho_0}^{\rho} \frac{P_S(\bar{\rho})}{\bar{\rho^2}}~\mathrm{d}\bar{\rho},\]

where \(A\), \(B\), \(C\), \(y\), and \(Z\) are all user-settable parameters and again quantities with a subcript of \(0\) refer to the reference state. The variable \(\bar{\rho}\) is simply an integration variable. The parameter \(C\) is especially useful for ensuring that the high-pressure portion of the shock Hugoniot does not cross that of the products.

The settable parameters are the dimensionless parameters listed above as well as the pressure, density, temperature, energy, Gruneisen parameter, and constant volume specific heat capacity at the reference state.

The constructor for the Davis Reactants EOS is

DavisReactants(const Real rho0, const Real e0, const Real P0, const Real T0,
               const Real A, const Real B, const Real C, const Real G0, const Real Z,
               const Real alpha, const Real Cv0)

where rho0 is \(\rho_0\), e0 is \(e_0\), P0 is \(P_0\), T0 is \(T_0\), A is \(A\), B is \(B\), C is \(C\), G0 is \(\Gamma_0\), Z is \(Z\), alpha is \(\alpha\), and Cv0 is the specific heat capacity at the reference state.

Davis Products EOS

Warning

Entropy is not yet available for this EOS

The Davis products EOS is created from the reference isentrope passing through the CJ state of the high explosive along with a constant heat capacity. The constant heat capacity leads to the energy being a simple funciton of the temperature deviation from the reference isentrope such that

\[e(\rho, T) = e_S(\rho) + C_{V,0} (T - T_S(\rho)).\]

The Gruneisen parameter is given by

\[\Gamma(\rho) = k - 1 + (1-b) F(\rho)\]

where \(b\) is a user-settable dimensionless parameter and \(F(\rho)\) is given by

\[F(\rho) = \frac{2a (\rho V_{\mathrm{C}})^n}{(\rho V_{\mathrm{C}})^{-n} + (\rho V_{\mathrm{C}})^n}.\]

Here the calibration parameters \(a\) and \(n\) are dimensionless while \(V_{\mathrm{C}}\) is given in units of specific volume.

Finally, the pressure, energy, and temperature along the isentrope are given by

\[P_S(\rho) = P_{\mathrm{C}} G(\rho) \frac{k - 1 + F(\rho)}{k - 1 + a}\]

\[e_S(\rho) = e_{\mathrm{C}} G(\rho) \frac{1}{\rho V_{\mathrm{C}}}\]

\[T_S(\rho) = T_{\mathrm{C}} G(\rho) \frac{1}{(\rho V_{\mathrm{C}})^{ba + 1}}\]

where

\[G(\rho) = \frac{ \left( \frac{1}{2}(\rho V_{\mathrm{C}})^{-n} + \frac{1}{2}(\rho V_{\mathrm{C}})^n \right)^{a/n}} {(\rho V_{\mathrm{C}})^{-(k+a)}}\]

and

\[e_{\mathrm{C}} = \frac{P_{\mathrm{C}} V_{\mathrm{C}}}{k - 1 + a}.\]

Here, there are four dimensionless parameters that are settable by the user, \(a\), \(b\), \(k\), and \(n\), while \(P_\mathrm{C}\), \(e_\mathrm{C}\), \(V_\mathrm{C}\) and \(T_\mathrm{C}\) are tuning parameters with units related to their non-subscripted counterparts.

Note that the energy zero (i.e. the reference energy) for the Davis products EOS is arbitrary. For the isentrope to properly pass through the CJ state of a reacting material, the energy release of the reaction needs to be accounted for properly. If done external to the EOS, an energy source term is required in the Euler equations. However, a common convention is to specify the reactants and product EOS in a consistent way such that the reference energy corresponds to the rest state of the material before it reacts.

The energy at the CJ state can be calculated as

\[e_\mathrm{CJ} = \frac{P_0 + P_\mathrm{CJ}}{2(V_0 - V_\mathrm{CJ})},\]

relative to \(e = 0\) at the reference state of the reactants. Therefore the energy offset of the products EOS is given by

\[e_0 = e_S(V_\mathrm{CJ}) - e_\mathrm{CJ}.\]

Practically, this means \(e_0\) should be positive for any energetic material.

To provide the energy offset to the Davis Products EOS, the energy shift modifier should be used. Note that the convention there is that the shift is positive, so \(-e_0\) should be provided to the shift modifier.

The constructor for the Davis Products EOS is

DavisProducts(const Real a, const Real b, const Real k, const Real n, const Real vc,
              const Real pc, const Real Cv)

where a is \(a\), b is \(b\), k is \(k\), n is \(n\), vc is \(V_\mathrm{C}\), pc is \(P_\mathrm{C}\), Cv is \(C_{V,0}\).

Spiner EOS

Warning

Entropy is not yet available for this EOS

Spiner EOS is a tabulated reader for the Sesame database of material equations of state. Materials include things like water, dry air, iron, or steel. This model comes in two flavors: SpinerEOSDependsRhoT and SpinerEOSDependsRhoSie. The former tabulates all quantities of interest in terms of density and temperature. The latter also includes tables in terms of density and specific internal energy.

Tabulating in terms of density and pressure means that computing, e.g., pressure in terms of density and internal energy requires solving the equation:

\[e_0 = e(\rho, T)\]

for temperature \(T\) given density \(\rho\) and specific internal energy \(e_0\). This is in general not closed algebraically and must be solved using a root-find. SpinerEOSDependsRhoT performs this root find in-line, and the result is performant, thanks to library’s ability to take and cache initial guesses. SpinerEOSDependsRhoSie circumvents this issue by tabulating in terms of both specific internal energy and temperature.

Both models use (approximately) log-linear interpolation on a grid that is (approximately) uniformly spaced on a log scale. Thermodynamic derivatives are tabulated and interpolated, rather than computed from the interpolating function. This approach allows for significantly higher fidelity approximations of these derivatives.

Both SpinerEOS classes benefit from a lambda parameter, as described in the EOS API section`. In particular, if an array of size 2 is passed in to the scalar call (or one per point for the vector call), the model will leverage this scratch space to cache initial guesses for root finds.

To avoid race conditions, at least one array should be allocated per thread. Depending on the call pattern, one per point may be best. In the vector case, one per point is necessary.

The constructor for SpinerEOSDependsRhoT is given by two overloads:

SpinerEOSDependsRhoT(const std::string &filename, int matid,
                     bool reproduciblity_mode = false);
SpinerEOSDependsRhoT(const std::string &filename, const std::string &materialName,
                     bool reproducibility_mode = false);

where here filename is the input file, matid is the unique material ID in the database in the file, materialName is the name of the material in the file, and reproducability_mode is a boolean which slightly changes how initial guesses for root finds are computed. The constructor for SpinerEOSDependsRhoSie is identical.

sp5 files and sesame2spiner

The SpinerEOS models use their own file format built on hdf5, which we call sp5. These files can be generated by hand, or they can be generated from the sesame database (assuming eospac is installed) via the tool sesame2spiner, which is packaged with singularity-eos. Buld sesame2spiner by specifying

-DSINGULARITY_USE_HDF5=ON -DSPINGULARITY_USE_EOSPAC=ON -DSINGULARITY_BUILD_SESAME2SPINER=ON

at configure time. The call to sesame2spiner is of the form

sesame2spiner -s output_file_name.sp5 input1.dat input2.dat ...

for any number of input files. Verbosity flags -p and -v are also available. Use -h for a help message. The -s flag is optional and the output file name defaults to materials.sp5.

Each input file corresponds to a material and consists of simple key-value pairs. For exampe the following input deck is for air:

matid = 5030
# These set the number of grid points per decade
# for each variable.
numrho/decade = 40
numT/decade = 40
numSie/decade = 40
# Defaults pulled from the sesame file if possible
name = air
rhomin = 1e-2
rhomax = 10
Tmin = 252
Tmax = 1e4
siemin = 1e12
siemax = 1e16
# These shrink the logarithm of the bounds by a fraction of the
# total inteval <= 1.
# Note that these may be deprecated in the near future.
shrinklRhoBounds = 0.15
shrinklTBounds = 0.15
shrinkleBounds = 0.5

Comments are prefixed with #. eospac uses environment variables and files to locate files in the sesame database, and sesame2spiner uses eospac. So the location of the sesame database need not be provided by the command line. For how to specify sesame file locations, see the eospac manual.

Piecewise Spiner Grids

sesame2spiner also supports grids with different resolutions in different parts of the table. We call these piecewise grids. By default grids are now piecewise. Piecewise grids can be disabled with

# defaults are true
piecewiseRho = false
piecewiseT = false
piecewiseSie = false

These options may be true or false. The default is true. When piecewise grids are active, the density-temperature (or density-energy) grid is built as a Cartesian product grid of grids of non-uniform resolutions. The density grid gets split into three pieces, a region [rhoMin, rhoFineMin], a region [rhoFineMin, rhoFineMax], and a region [rhoFineMin, rhoMax]. The numrho/decade parameter sets the number of points per decade in the central refined region. The regions at lower and higher density have rhoCoarseFactorLo and rhoCoarseFactorHi fewer points per decade respectively compared to the finer region.

Typically the fine region should be roughly centered around the normal density for a material, which is usually a challenging region to capture. If you neglect to set rhoFineMin and rhoFineMax, sesame2spiner will set the central refined region to be a region of diameter rhoFineDiameterDecades (in log space) around the material’s normal density.

The temperature grid has two regions, a more finely spaced region at low temperatures and a less finely spaced region at high temperatures. The regions are spearated by a temperature TSplitPoint. The default is \(10^4\) Kelvin. The energy grid follows the temperature grid, with the energy split point corresponding to the temperature split point. The coarser high-temperature temperature and energy grids are coarsened by a factor of TCoarseFactor and sieCoarseFactor respectively.

A diagram of a density-temperature grid is shown below. The region with temperatures below TSplitPoint is refined in temperature. The region between rhoFineMin and rhoFineMax is refined in density.

Thus the input block for piecewise grid might look like this:

# Below, all right-hand-sides are set to their default values.
piecewiseRho = true
piecewiseT = true
piecewiseSie = true

# the fine resolution for rho.
numrho/decade = 350
# width of the fine region for rho
rhoFineDiameterDecades = 1.5
# the lower density region is 3x less refined
rhoCoarseFactorLo = 3
# the higher density region is 5x less refined
rhoCoarseFactorHi = 5

# the fine resolution for T
numT/decade = 100
# the point demarking the coarse and fine regions in temperature
TSplitPoint = 1e4
# it's usually wise to to not let
# temperature get too small in log space if you do this
Tmin = 1
# The coarser region (above the split point) is 50 percent less refined
TCoarseFactor = 1.5

# energy has the split point sie(rhonormal, TSplitPoint)
# but we may still specify the resolution
numSie/decade = 100
sieCoarseFactor = 1.5

Note

For all grid types, the only required value in an input file is the matid. Table bounds and normal density will be inferred from the sesame metadata if possible and if no value in the original input file is provided. Table densities and positions and sizes of refined regions are not inferred from the table, but are chosen with the default values listed in the above code block.

Note

Both the flat and hierarchical grids attempt to align their grids so that there is a grid point in density and temperature exactly at room temperature and normal density. This is because normal density and room temperature is a particularly important point in phase space, as it is the point in phase space a piece of material sitting on your desk would be at. This is called an anchor point for the mesh.

SAP Polynomial EOS

This model is specific to the Safety Applications Project (SAP). It is an incomplete EOS, and is a simple analytical form used to fit experimental data:

\[P = a_0 + a_1\mu + a_2^* \mu^2 + a_3 \mu^3 + \varepsilon(b_0 + b_1\mu + b_2^*\mu^2 + b_3\mu^3)\]

with

\[\mu = \frac{\rho}{\rho_0} - 1\]

The constants \(a_2^*\) and \(b_2^*\) can assume different values in expansion and compression.

\[\begin{split}a_2^* = \begin{cases} a_2^c & \mu \geq 0 \text{ (compression)}\\ a_2^e & \mu < 0 \text{ (expansion)}\\ \end{cases}\end{split}\]

and similar expressions for \(b_2^*\).

Stellar Collapse EOS

This model provides finite temperature nuclear equations of state suitable for core collapse supernova and compact object (such as neutron star) simulations. These models assume nuclear statistical equilibrium (NSE). It reads tabulated data in the Stellar Collapse format, as first presented by OConnor and Ott.

Like SpinerEOSDependsRhoT, StellarCollapse tabulateds all quantities in terms of density and temperature on an (approximately) logarithmically spaced grid. And similarly, it requires an in-line root-find to compute quantities in terms of density and specific internal energy. Unlike most of the other models in singularity-eos, StellarCollapse also depends on a third quantity, the electron fraction,

\[Y_e = \frac{n_e}{n_p + n_n}\]

which measures the number fraction of electrons to baryons. Symmetric matter has a \(Y_e\) of 0.5, while cold neutron stars, have a \(Y_e\) approximately less than 0.1.

As with SpinerEOSDependsRhoT, the Stellar Collapse tables tabulate thermodynamic derivatives separately, rather than reconstruct them from interpolants. However, the tabulated values can contain artifacts, such as unphysical spikes. To mitigate this issue, the thermodynamic derivatives are cleaned via a median filter. The bulk modulus is then recomputed from these thermodynamic derivatives via:

\[B_S(\rho, T) = \rho \left(\frac{\partial P}{\partial\rho}\right)_e + \frac{P}{\rho} \left(\frac{\partial P}{\partial e}\right)_\rho\]

Note that StellarCollapse is a relativistic model, and thus the sound speed is given by

\[c_s^2 = \frac{B_S}{w}\]

where \(w = \rho h\) for specific entalpy \(h\) is the enthalpy by volume, rather than the density \(rho\). This ensures the sound speed is bounded from above by the speed of light.

The StellarCollapse model requires a lambda parameter of size 2, as described in the EOS API section`. The zeroth element of the lambda array contains the electron fraction. The first element is reserved for caching. It currently contains the log of the temperature, but this should not be assumed.

To avoid race conditions, at least one array should be allocated per thread. Depending on the call pattern, one per point may be best. In the vector case, one per point is necessary.

The StellarCollpase model can read files in either the original format found on the Stellar Collapse website, or in the sp5 format described above.

Warning

Note that the data contained in an sp5 file for the StellarCollapse EOS and the SpinerEOS models is not identical and the files are not interchangeable.

The constructor for the StellarCollapse EOS class looks like

StellarCollapse(const std::string &filename, bool use_sp5 = false,
                bool filter_bmod = true)

where filename is the file containing the tabulated model, use_sp5 specifies whether to read an sp5 file or a file in the original Stellar Collapse format, and filter_bmod specifies whether or not to apply the above-described median filter.

StellarCollapse also provides

void Save(const std::string &filename)

which saves the current EOS data in sp5 format.

The StellarCollapse model, if used alone, also provides several additional functions of interest for those running, e.g., supernova simulations:

void MassFractionsFromDensityTemperature(const Real rho, const Real temperature, Real &Xa, Real &Xn, Real &Xp, Real &Abar, Real &Zbar, Real *lambda = nullptr) const

which returns the mass fractions for alpha particles, Xa, heavy ions Xh, neutrons Xn, and protons Xp, as well as the average atomic mass Abar and atomic number Zbar for heavy ions, assuming nuclear statistical equilibrium.

In addition, the user may query the bounds of the table via the functions rhoMin(), rhoMax(), TMin(), TMax(), YeMin(), YeMax(), sieMin(), and sieMax(), which all return a Real number.

Warning

As with the SpinerEOS models, the stellar collapse models use fast logs. You can switch the logs to true logs with the SINGULARITY_USE_TRUE_LOG_GRIDDING cmake option.

Note

A more performant implementation of fast logs is available, but it might not be portable. Enable it with the SINGULARITY_USE_HIGH_RISK_MATH cmake option.

Helmholtz EOS

This is a performance portable implementation of the Helmholtz equation of state provided by Timmes and Swesty. The Helmholtz EOS is a three part thermodynamically consistent EOS for a hot, ionized gas. It consists of a thermal radiation term:

\[P = \sigma \cdot T^4\]

an ions term, treated as an ideal gas:

\[P = (\gamma - 1) \cdot \rho \cdot e\]

and a degenerate electron term. Additionally, coulomb force corrections can be applied on top of the full model. This multi-component model depends on the relative abundances of electrons and ions, as well as the atomic mass and charge of the ions. As such, the Helmholtz EOS requires two additional indepenent variables, the average atomic mass, Abar, and the average atomic number, Zbar. These are passed in through the lambda pointer. As with the other tabulated EOS’s, the log of the temperature is also stored in the lambda pointer as a cache for root finding. Helmholtz provides an enum for indexing into the lambda:

• Helmholtz::Lambda::Abar indexes into the Abar component of the lambda array.

• Helmholtz::Lambda::Zbar indexes into the Zbar component of the lambda array.

• Helmholtz::Lambda::lT indexes into the log temperature cache inside the lambda array.

The degenerate electron term is computed via thermodynamic derivatives of the Helmholtz free energy (hence the name Helmholtz EOS). The free energy is pre-computed via integrals over the Fermi sphere and tabulated in a file provided from Frank Timmes’s website.

The table is a simple small ascii file. To ensure thermodyanic consistency, the table is interpolated using either biquintic or bicubic Hermite polynomials, which are sufficiently high order that their high-order derivatives match the underlying data.

Warning

Only a modified version of the table is supported due to the fixed number of colums in the table. This may change in the future. The original table found on Frank Timmes’s website is not supported. A compatible version of the table can be found in the data/helmholtz directory of the source code, or the data directory specified in the installation configuration.

Note

The implication of interpolating from the free energy is that each EOS evaluation provides ALL relevant EOS data and thermodynamic derivatives. Thus the per-quantity EOS calls are relatively inefficient, and it is instead better to use the FillEos call to get the entire model at once.

The Helmholtz EOS is instantiated by passing in the path to the relevant table:

Helmholtz(const std::string &filename)

Note that e.g. the Gruneisen parameter is defined differently compared to other EOSs. Here the Gruneisen parameter is the \(\Gamma_3\) of Cox & Giuli 1968 - Princiiples of Stellar Structure (c&g in the following). Specifically:

\[\Gamma_3 - 1 = \left. \frac{\mathrm{d} \ln T}{ \mathrm{d} \ln \rho}\right|_\mathrm{ad}\]

Some important formulas to be used when using this EOS:

• the temperature and density exponents (c&g 9.81 9.82)

• the specific heat at constant volume (c&g 9.92)

• the third adiabatic exponent (c&g 9.93)

• the first adiabatic exponent (c&g 9.97)

• the second adiabatic exponent (c&g 9.105)

• the specific heat at constant pressure (c&g 9.98)

• and relativistic formula for the sound speed (c&g 14.29)

The constructor for the Helmholtz EOS class looks like

Helmholtz(const std::string &filename, const bool rad = true,
          const bool gas = true, const bool coul = true,
          const bool ion = true, const bool ele = true,
          const bool verbose = false, const bool newton_raphson = true)

where filename is the file containing the tabulated model. The optional arguments rad, gas, coul, ion, and ele specify whether to include the radiation, ideal gas, coulomb correction, ionization, and electron contributions, respectively. The default is to include all terms. The optional argument verbose specifies whether to print out additional information, e.g. when the root find fails to converge. The optional argument newton_raphson specifies whether to use the Newton-Raphson method or the regula falsi method for root finding. The default is to use the Newton-Raphson method (note that the regula falsi method is used as a fallback in case the Newton-Raphson method does not converge).

EOSPAC EOS

Warning

Entropy is not yet available for this EOS

This is a striaghtforward wrapper of the EOSPAC library for the Sesame database. The constructor for the EOSPAC model looks like

EOSPAC(int matid, bool invert_at_setup = false, Real insert_data = 0.0, eospacMonotonicity monotonicity = eospacMonotonicity::none, bool apply_smoothing = false, eospacSplit apply_splitting = eospacSplit::none, bool linear_interp = false)

where matid is the unique material number in the database, invert_at_setup specifies whether or not pre-compute tables of temperature as a function of density and energy, insert_data inserts specified number of grid points between original grid points in the Sesame table, monotonicity` enforces monotonicity in x, y or both (:math:`monotonicityX/Y/XY`), ``apply_smoothing enables data table smoothing that imposes a linear floor on temperature dependence, forces linear temperature dependence for low temperature, and forces linear density dependence for low and high density, apply_splitting has the following options for ion data tables not found in the Sesame database :. \(splitNumProp\) uses the cold curve plus number-proportional model, \(splitIdealGas\) uses the cold curve plus ideal gas model and \(splitCowan\) uses the cold curve plus Cowan-nuclear model for ions and the final option linear_interp uses linear instead of bilinear interpolation.

Note for performance reasons this EOS uses a slightly different vector API. See EOSPAC Vector Functions for more details.