SURFACE
Defines a boundary, interface, or geometry for a selected mesh object.
Surfaces are used to create geometry REGION and material regions MREGION for a mesh object.
Mesh interfaces will be assigned node constraint (icr) values corresponding to the surfaces on which nodes sit.
The command SETTETS will generate parent/child node chains (isn) for nodes on intrface or intrcons surfaces.
The inside/outside conventions for sheet surfaces are described below.
SYNTAX
surface/isurname/ ibtype / istype / istype_parameters surface/isurname/release
isurname is the name of the surface and must be unique for each surface defined for the current mesh object.
release will release the previously defined surface referenced by name. All references will be removed from the geometry data structures and all constraints (icr) values associated with this surface will be removed.
Options for ibtype
These options define the boundary type and constraints.
free unconstrained, exterior
reflect constrained, exterior, assigned constraint values (icr).
intrface unconstrained, interior, will generate parent/child node chains (isn).
intrcons constrained, internal, are assigned constraint values (icr) and will generate parent/child node chains (isn).
virtual constrained, internal surfaces which have different materials on either side of the virtual interfaces do not
separate material regions but are intended to identify other structural features of a geometry. Nodes on this surface will be assigned constraint values (icr).
Options for istype
istype are types of surfaces represented by geometric shapes. Each type has parameters specific to its geometry.
box / xmin,ymin,zmin / xmax,ymax,zmax is a cube defined by min and max coordinates, i.e bottom left and top right corners.
cylinder / x1,y1,z1/x2,y2,z2/radius is a cylinder defined by point 1 bottom center and point 2 top center. The radius is the length from center to cylinder edge. Cylinders are open but finite. To create a closed cylinder cap both ends with planes.
cone / x1,y1,z1/x2,y2,z2/radius is a cone where point 1 is the vertex and point 2 is the base center of the cone with radius from that point. A cone is finite but does have an open end. To create a closed cone cap the open end with a plane.
ellipse / x1,y1,z1 / x2,y2,z2 / x3,y3,z3 / ar,br,cr is an ellipse point 1 is the center of the ellipsoid and point 2 is on the a semi-axis (new x), point 3 is on the b semi-axis (new y). The values ar, br, cr are radii on their respective semi-axes.
parallel / x1,y1,z1 / x2,y2,z2 / x3,y3,z3 / x4,y4,z4 is a parallel piped where points 1, 2, 3 are the front left, front right and back left points of the base and point 4 is the upper left point of the front face.
plane or planexyz / x1,y1,z1 / x2,y2,z2 / x3,y3,z3 is a plane defined by 3 coordinate points. The direction normal to the plane is determined by the order of the points according to the right hand rule.
planertz / radius1, theta1, z1, radius2, theta2, z2, radius ,zcen is a plane defined by cylindrical coordinate system.
planertp / radius1,theta1,phi1, radius2,theta2,phi2, radius3,theta3,phi3/ xc, yc, zc is a plane defined by spherical coordinate system.
sphere / xc, yc, zc, radius is a sphere defined by the center point and the radius distance from center point to sphere surface.
sheet / cmo_name is a surface defined by a mesh object that is a 2D quad or triangle connected mesh. See inside/outside conventions below for a description of inside/outside or left/right with respect to sheet surfaces.
tabular / x1,y1,z1/x2,y2,z2/ rz or rt / is a rotated tabular profile where point 1 and point 2 define the axis of rotation for the tabular profile with point 1 as the origin. This is followed by pairs of profile descriptors depending on the value of rz or rt. If rz, then the r value is a radius normal to the axis of rotation and z is the distance along the new axis of rotation. If set to rt then theta is the angle from the axis of rotation at point 1 and r is the distance from point 1 along theta. The first pair must start on a new line and all lines must contain pairs of data. The last pair of data must be followed by end.
surface/s_name/ibtype/tabular / x1,y1,z1 / x2,y2,z2 / rz / & r1,z1 & r2,z2 & .... rn,zn & end or surface/s_name/ibtype/tabular / x1,y1,z1 / x2,y2,z2 / rt / & r1,theta1 & r2,theta2 & ... rn,thetan & end
EXAMPLES
surface / s_box / reflect / box / -1. -1. -1. / 1. 1. 1.
region/ r_box / le s_box
Define a region inside or equal to a box with lower left corner (-1. -1. -1.) and upper right corner at (1. 1. 1.).
read avs surfmesh_input.inp mosurf
cmo/select/motet
surface/surf_bndry/intrface/sheet/mosurf
region/ rout / ge surf_bndry
eltset/ eout / region / rout
Read a triangulated surface to truncate a mesh. Use the surface to find elements outside the surface and name the set “eout”.
surface / s_cone / reflect / cone / .1 .1 .1 / .5 .5 .5 / .3
Define a cone surface with tip at (.1 .1 .1) and center at (.5 .5 .5) with .3 radius.
define XC 498.0
define YC 539.0
define ZBOT -500.0
define ZTOP 500.0
define RAD 42.0
surface/ s_cyl /intrface/cylinder/XC,YC,ZBOT/XC,YC,ZTOP/ RAD
Use define variables to create a cylinder shaped surface.
surface / s_ellipse / reflect / ellipse / &
552250.0 4121975.0 1275.0 / &
552251.0 4121975.0 1275.0 / &
552250.0 4121976.0 1275.0 / &
500.0 225.0 125.0
region / r_ellipse / le s_ellipse
eltset/ereset/region/r_ellipse
Define an ellipsed shaped region and select elements.
define x1 497000.
define y1 540612.
define x2 499300.
define y2 540100.
define x3 497000.
define y3 541316.
surface/SSBOX/intrface/parallel/x1,y1,1700./ &
x2,y2,1700./x3,y3,1700./x1,y1,5000./
define x1 499029.5961
define x2 500174.3616
define y1 538579.7712
define y2 539378.5612
define uleft 1779.9725
define uright 1778.7472
define lleft 1779.7481
define lright 1778.5228
surface/ swtr / intrface /plane/ x2, y1, lright / x2, y2, uright / x1, y2, uleft
surface / bbox / reflect / box / .1 .1 .1 / .9 .9 .9
surface / s1 / intrface / sheet / cmo_2
surface / s2 / intrface / sheet / cmo_3
region / r1 / lt bbox and gt s1 and gt s2
region / r2 / lt bbox and gt s1 and lt s2
region / r3 / lt bbox and lt s1 and gt s2
region / r4 / lt bbox and lt s1 and lt s2
Set up a parallel piped and plane surfaces then define sheet surfaces from the triangulations in cmo_2 and cmo_3. Define geometry regions relative to the surfaces.
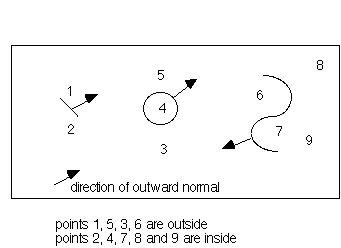
Sheet surfaces inside/outside Convention
Inside/outside will be determined by the following algorithm:
-
For the point being considered, p, find the nearest sheet triangle and the closest point, q, to p that lies on that triangle.
-
Construct the vector
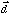 , from q to p.
, from q to p. -
Construct the outward normal to the triangle,
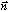
The outward normal is constructed using the right hand rule and the order of the points in the sheet. Sheets may be specified as quad Mesh Object (i.e. a 2 dimensional array of points containing the coordinates of the corners of each quad). Either two triangles (divide each quad in two using point (i,j) and (i+1,j+1)) or four triangles (add a point in the center of the quad) are generated by each quad. Applying the right hand rule to the points (i,j), (i+1,j), (i+1,j+1) gives the direction of the normal for all triangles created from the quad.
-
If
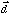
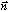 < 0 then
the point is inside. If
< 0 then
the point is inside. If 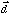
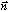 >0 the
point is outside. If
>0 the
point is outside. If 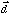
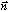 * n = 0, and if
p is on the triangle then p=q and p in on the triangle.
* n = 0, and if
p is on the triangle then p=q and p in on the triangle. -
If
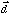
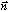 = 0 and p is not on the triangle then p is outside.
= 0 and p is not on the triangle then p is outside.
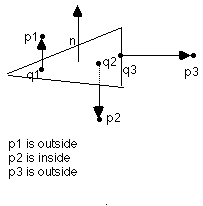
One implication of this definition is that the concept of shadows cast by open sheets no longer is valid. Sheets may be considered to extend to the boundary of the geometry.