Generation Methods

SimFrac has multiple generation methods to produce rough fracture surfaces. The methods can be broken into two primary categories. The first set of techniques are spectral methods that produces self-affine/fractal surfaces. The section set are convolution-based. Below we discuss each of the methods and provide examples of each. In addition to generating synthetic fractures, SimFrac can be used to read in profilometry of fracture surfaces obtained in the laboratory.

SimFrac Object

Each surface is a SimFrac object.

class pysimfrac.src.general.SimFrac(lx=None, ly=None, h=None, nx=None, ny=None, shear=None, method=None, units=None, pickle_file=None)

The SimFrac Object

Parameters:

• self (simFrac Object) –

• units (string) – SI units for domain size, e.g., mm

• lx (float) – Length of domain in x direction

• ly (float) – Length of domain in x direction

• h (float) – Dicretization length of domain. Uniform in x and y

• nx (int) – Number of nodes in x

• ny (int) – Number of nodes in y

• shear (float) – Shear to apply in x direction

• method (string) – name of generation method. Options are “spectral”, “Gaussian”, or “box”

• pickle_file (string) – Name of pickled simFrac object. If a value is provided. The object will be loaded from file.

Return type:

None

Notes

• If nx and ny are provided, the resulted hx and hy must be the same.

myFrac = SimFrac(h = 0.01, lx = 1, ly = 1,
                method = "spectral",
                units = 'mm')

Spectral

Method Description

Rough fracture surfaces have been represented by fractal/self-affine models. At a first order approximation, The Fourier decomposition of a rough surface indicates that many non-uniform surfaces exhibit a power spectral density function of the form

\[G(k) = C k^{-\alpha}\]

where \(k = 2 \pi/\lambda\) is the wave number/Fourier mode, \(\lambda\) is the wavelength, \(C\) is a proportionality constant, and \(\alpha\) is the decay exponent. Based on these observations, a number of spectral/Fourier based rough surface generation methods have been proposed, the most common being (Brown 1995), (Glover et al. 1998), and (Ogilvie et al. 2006).

While there are differences and chronological improvements between these method, the core portion of the algorithms are fairly consistent. The methods all modify the amplitude and phases of the Fourier components of the surfaces. The amplitudes are scaled according to the equation above and the phases are controlled using streams of random numbers. Special care is taken to define the random numbers which define phase, see Ogilvie et al. 2006 for a detailed discussion. The desired fractal dimension and autocorrelation of the surface is often defined in terms of the Hurst exponent which is in a particular sense related to \(\alpha\) in the equation above. These features along with anisotropy are included into the method via the amplitudes of the decomposition. The spectral method implemented in pySimFrac has the following parameters

1. Mean aperture value; range \(\gt 0\)

2. Roughness/standard deviation of heights; range \(\geq 0\)

3. Hurst exponent with range; range (0,1)

4. Anisotropy ratio; range (0,1)

5. \(\lambda_0\) roll-off length scale as a fraction of fracture size; range [0,1]

6. Mismatch length scale (wavelength) as a fraction of fracture size [0,1]

7. Power spectral density model roll-off function (linear/bilinear/smooth)

Example

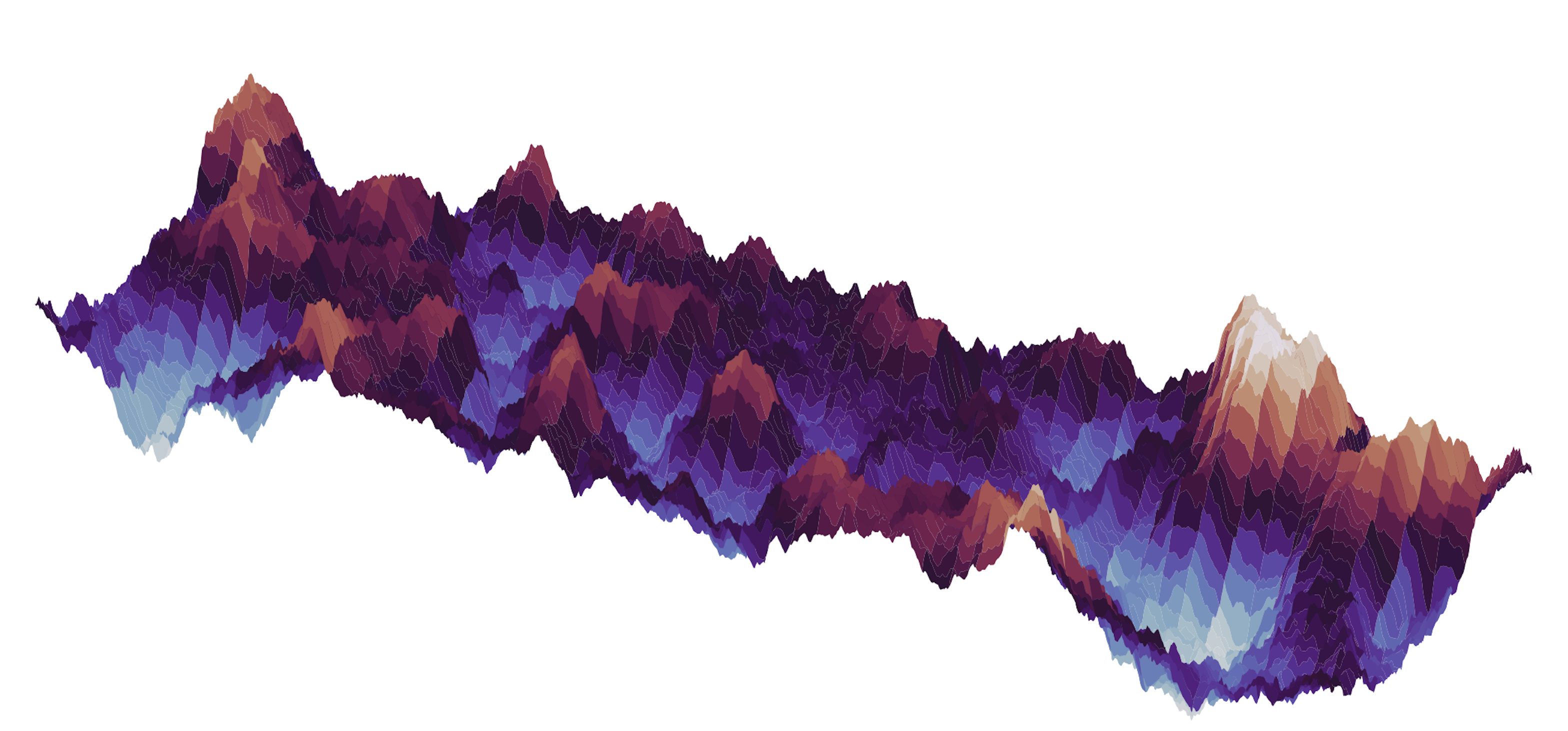
Spectral = SimFrac(h = 0.01, lx = 3, ly = 1,
                method = "spectral",
                units = 'mm')

Spectral.params["roughness"]["value"] = 0.05
Spectral.params["mean-aperture"]["value"] = 1.0
Spectral.params["H"]["value"] = 0.5
Spectral.params["aniso"]["value"] = 0.5
Spectral.params["mismatch"]["value"] = 0.1
Spectral.params["model"]["value"] = "smooth"
Spectral.create_fracture()

Fracture surface generated using the spectral method

Source code

pysimfrac.src.methods.spectral.check_spectral_parameters(self)

Check that all required parameters for spectral field generation are provided. Exits if not.

Parameters:

object (simfrac) –

Return type:

None

Notes

None

pysimfrac.src.methods.spectral.create_spectral(self)

Generate a fracture surface using the spectral method.

Parameters:

self (simfrac object) –

Return type:

None

Notes

This method initializes the spectral method parameters, checks the parameters for consistency, and generates a fracture surface using the spectral method.

pysimfrac.src.methods.spectral.initialize_spectral_parameters(self)

Initializes parameters used in method spectral for fracture surface generation

Parameters:

object (simFrac) –

Return type:

None

Notes

Attaches dictionary with parameters onto the simfrac object

For theoretical details see: “Brown, Simple mathematical model of a rough fracture, J. of Geophysical Research, 100 (1995): 5941-5952” “Glover et al., Synthetic rough fractures in rocks, J. of Geophysical Research, 103 (1998): 9609-9620” “Glover et al., Fluid flow in synthetic rough fractures and application to the Hachimantai geothermal hot dry rock test site, 103 (1998): 9621-9635”

Convolution

The convolution methods are based on creating a stationary random topography by convolving an uncorrelated random field \((u(x)) \sim U[0,1])\) with a specified kernel \((k(x))\)

\[T(x) = \int dy~k(x - y) \ast u(x).\]

The structure of the \(T(x)\) (moments, correlation, and anisotropy) are determined by the central limit theorem and the properties of the kernel. pySimFrac has several built in kernels.

The convolution method implemented in pySimFrac has the following parameters

1. Mean Aperture

2. Aperture Log-Variance

3. \(\lambda_x\) Correlation length in \(x\) direction

4. \(\lambda_y\) Correlation length in \(y\) direction

Gaussian

Method Description

The primary kernel is a multi-variant 2-dimensional Gaussian function of the form

\[k(x) = \frac{1}{2 \pi \sqrt{Det(\Lambda)}}\exp\left [ -x^\prime \Lambda x/2 \right]\]

Example

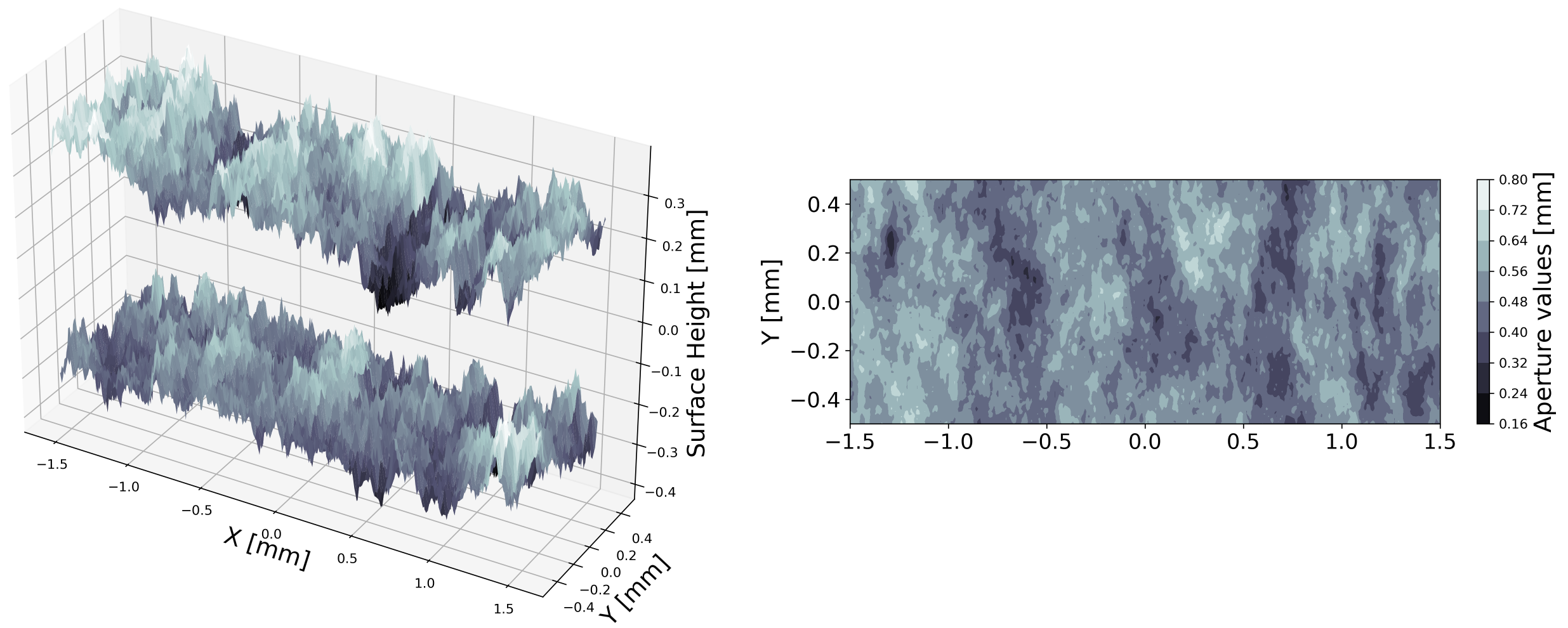
Gaussian = SimFrac(method = "gaussian", h= 0.01, lx = 3, ly = 1, units = 'mm')
Gaussian.mean_aperture = 0.5
Gaussian.params["mean-aperture"]["value"] = 0.5
Gaussian.params["aperture-log-variance"]["value"] = 0.01
Gaussian.params["lambda_x"]["value"] = 0.15
Gaussian.params["lambda_y"]["value"] = 0.25
Gaussian.shear = 0.5
Gaussian.create_fracture()

Example Figure:

Fracture surface generated using the convolution method and the Gaussian kernel

Source code

pysimfrac.src.methods.gaussian.check_gaussian_parameters(self)

Check that all required parameters for Gaussian field generation are provided. Exits if not.

Parameters:

object (simfrac) –

Return type:

None

Notes

None

pysimfrac.src.methods.gaussian.create_gaussian(self)

Main generator of random fields following method described by Zinn and Harvey, 2003.

Parameters:

object (simfrac) –

Return type:

None

Notes

None

pysimfrac.src.methods.gaussian.initialize_gaussian_parameters(self)

Initializes parameters used in method gaussian for fracture surface generation

Parameters:

Object (simFrac) –

Return type:

None

Notes

Attaches dictionary with parameters onto the simfrac object

Box

Method Description

In addition to the Gaussian kernel, there is a uniform or box function kernel available in pySimFrac, and the inclusion of additional kernels is straightforward and an area of active development.

Example

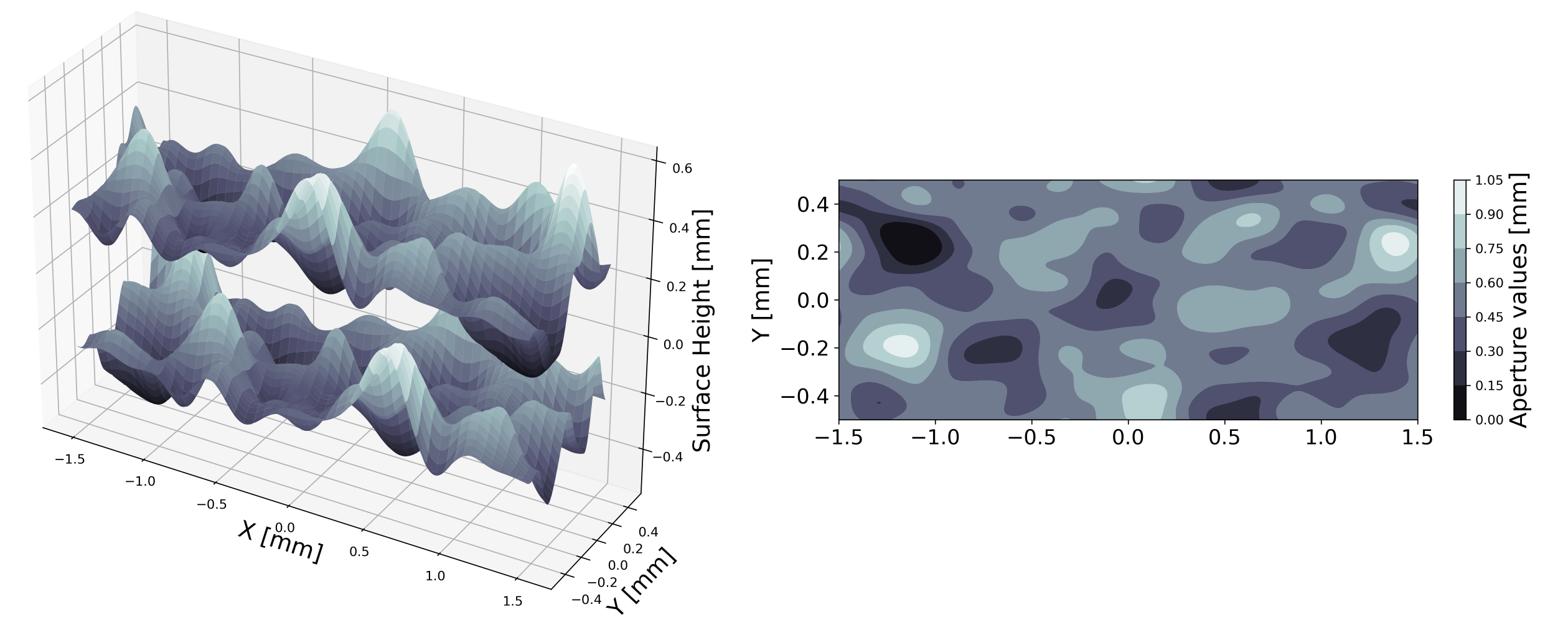
Gaussian = SimFrac(method = "box", h= 0.01, lx = 3, ly = 1, units = 'mm')
Gaussian.mean_aperture = 0.5
Gaussian.params["mean-aperture"]["value"] = 0.5
Gaussian.params["aperture-log-variance"]["value"] = 0.01
Gaussian.params["lambda_x"]["value"] = 0.15
Gaussian.params["lambda_y"]["value"] = 0.25
Gaussian.shear = 0.5
Gaussian.create_fracture()

Source code

pysimfrac.src.methods.box.check_box_parameters(self)

Check that all required parameters for Gaussian field generation are provided. Exits if not.

Parameters:

object (simfrac) –

Return type:

None

Notes

None

pysimfrac.src.methods.box.create_box(self)

Box Kernel for convolution

Parameters:

object (simfrac) –

Return type:

None

Notes

For theoretical details see “Hyman, Jeffrey D., and C. Larrabee Winter. “Stochastic generation of explicit pore structures by thresholding Gaussian random fields.” Journal of Computational Physics 277 (2014): 16-31.”

pysimfrac.src.methods.box.initialize_box_parameters(self)

Initializes parameters used in method box for fracture surface generation

Parameters:

Object (simFrac) –

Return type:

None

Notes

Attaches dictionary with parameters onto the simfrac object

Combination

Method Description

In addition to the base generation methods detailed above, there are a number of functions in pySimFrac to further manipulate the surfaces. Foremost, one can rescale the mean and variance of the surfaces, jointly or individually, and the mean projected aperture field using any desired value. Next, one can apply horizontal shear to the fracture by shifting the top fracture surface along the x-axis for the desired distance. A key property of the pySimFrac fractures is that they are periodic in both x and y and the shear effectively translates the surface around a torus. Thus, the shear translation does not introduce discontinuities in the surfaces nor shorten the domain size, which could be the case if the surface was not periodic. Maintaining periodicity in x and y is often an important requirement of numerical simulation, particularly when simulating steady state fluid distributions for relative permeability calculations. Finally, pySimFrac surfaces can be combined using weighted linear superposition to create new surfaces.

Example

An example of this is shown in the example Figure. Here, we combined the surfaces shown in the Figures for the Spectral and Gaussian methods with 1/4 and 3/4 weights, respectively. The resulting fracture surface inherits the long correlations from the Gaussian kernel convolution surface as well as the local roughness of the spectral method. Any number of fracture objects can be combined.

Combined = Spectral.combine_fractures([Gaussian], weights = [0.25, 0.75])

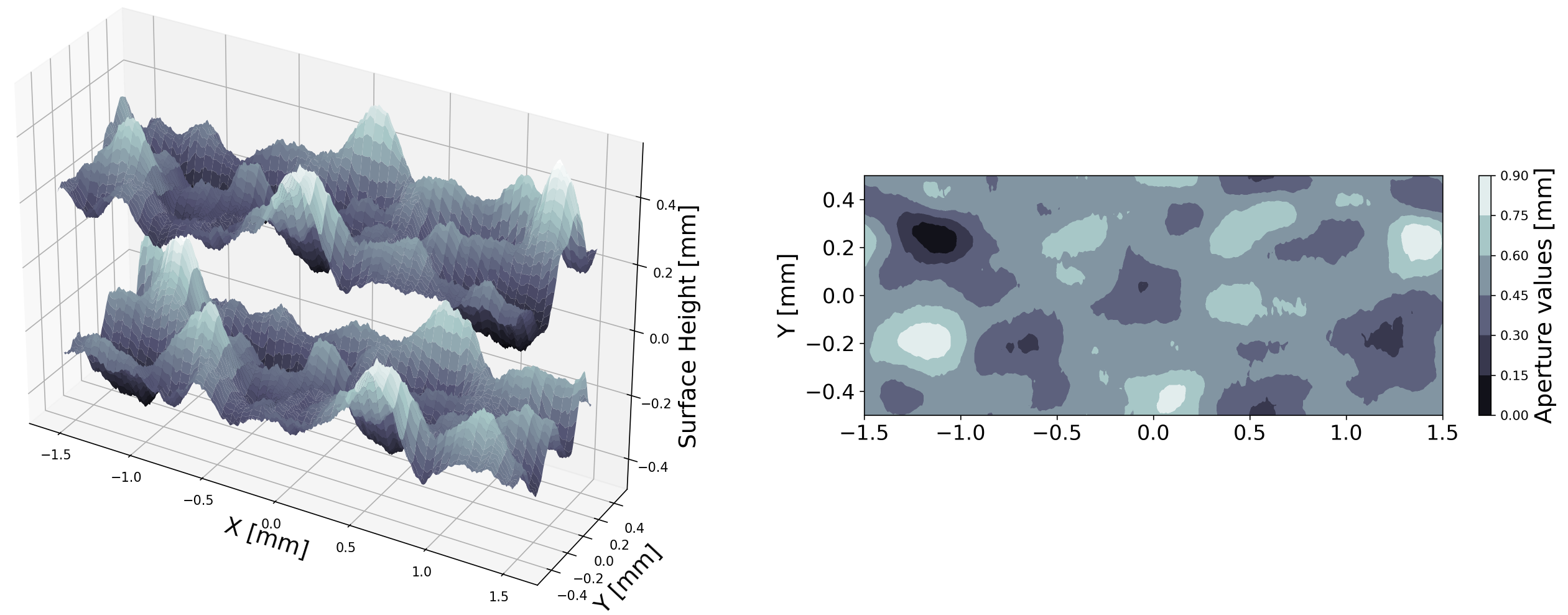
Fracture surface generated using the combined method

Source code

pysimfrac.src.methods.combine_fractures.combine_fractures(self, fracture_list, weights=None)

Combines multiple fracture surfaces using a point wise weighted linear superposition. Each point on the new fracture surface is the weighted summation of the points in the provided surfaces.

Parameters:

• fracture_list (list) – List of simfrac objects

• weights (list) – List of floats for weighting in superposition. The length must match that of fracture_list

Returns:

combined_fracture_list

Return type:

simfrac object

Notes

• All entries of fracture_list (simfrac objects) must have the same size and dimension.

• If the weights are not normalizes, sum to 1, then the are normalized in proporiton.

• If no weights are provided, the weights are set to be equal