3. AMG2023
This is the documentation for Benchmark - parallel algebraic multigrid solver for 3D diffusion problems.
3.1. Purpose
The AMG2023 benchmark consists of a driver (amg.c), a simple Makefile, and documentation. It is available at https://github.com/LLNL/AMG2023 . It requires an installation of hypre 2.30.0 or higher. It uses hypre’s parallel algebraic multigrid (AMG) solver BoomerAMG in combination with a Krylov solver to solve two linear systems arising from diffusion problems on a cuboid discretized by finite differences. The problems are set up through hypre’s linear-algebraic IJ interface. The problem sizes can be controlled from the command line.`.
3.2. Characteristics
3.2.1. Problems
Problem 1 (default): The default problem is a 3D diffusion problem on a cuboid with a 27-point stencil. It is solved with AMG-GMRES(100).
Problem 2 (-problem 2): This problem solves a 3D Laplace problem on a cuboid with a 7-point stencil. It is solved with AMG-PCG using one level of aggressive coarsening.
The problem sizes for both problems can be set by the user from the command line.
3.2.2. Figure of Merit
The figure of merit (FOM) is calculated using the total number of nonzeros for all system matrices and interpolation operators on all levels of AMG (NNZ), AMG setup wall clock time (Setup_time), and AMG solve phase wall clock time (Solve_time). Since in time dependent problems the AMG preconditioner might be used for several solves before it needs to be reevaluated, a parameter k has also been included to simulate computation of a time dependent problem that reuses the preconditioner for an average of k time steps.
The total FOM is evaluated as follows: FOM = NNZ / (Setup_time + k * Solve_time). The parameter k is set to 1 in Problem 1 and to 3 in Problem 2.
3.3. Source code modifications
Please see Run Rules Synopsis for general guidance on allowed modifications. For AMG2023, we define the following restrictions on source code modifications:
AMG2023 uses Hypre as the solver library, available at https://github.com/hypre-space/hypre . While source code changes to Hypre can be proposed, Hypre in AMG2023 may not be replaced with any other library.
Solver parameters should remain unchanged (smoothers, coarsening, etc.). AMG2023 uses the default Hypre parameters appropriate for each platform.
3.4. Building
The AMG2023 benchmark uses a simple Makefile system for building the driver.
It requires an installation of hypre 2.30.0 or higher, which can be downloaded from https://github.com/hypre-space/hypre via
git clone -b v2.30.0 https://github.com/hypre-space/hypre.git
Information on how to install hypre is available here: https://hypre.readthedocs.io/en/latest/
Depending on the machine and desired programming models, different configurations are needed. hypre configure options can be obtained by typing
./configure --help
in hypre’s src directory.
When using CPUs only, hypre generally can be installed by typing
./configure;make install
in the src directory.
If OpenMP threading within MPI tasks is desired, it should be configured as follows:
./configure --with-openmp --enable-hopscotch
If hypre should be run on Nvidia GPUs:
./configure --with-cuda
or
./configure --with-cuda --with-device-memory-pool
to use the memory pool option included with hypre.
If hypre is to be run on AMD GPUs:
./configure --with-hip --with-gpu-arch=gfx90a
--with-MPI-lib-dirs="${MPICH_DIR}/lib" --with-MPI-libs="mpi"
--with-MPI-include="${MPICH_DIR}/include"
If the problem to be run is larger than 2 billion, i.e., Px*Py*Pz*nx*ny*nz is larger than 2 billion, where Px*Py*Pz is the total number of MPI tasks and nx*ny*nz the local problem sizeper MPI task, hypre needs to be configured with
--enable-mixed-int
since it requires 64-bit integers for some global variables. By default, hypre uses 32-bit integers.
To build the code, first modify the ‘Makefile’ file appropriately,
then type
make
Other available targets are
make clean (deletes .o files)
make distclean (deletes .o files, libraries, and executables)
3.5. Running
The driver for AMG2023 is called ‘amg’. Type
amg -help
to get usage information. This prints out the following:
Usage:
amg [<options>]
-problem <ID>: problem ID
1 = solves 1 problem with AMG-PCG (default)
2 = solves 1 problem AMG-GMRES(100)
-n <nx> <ny> <nz>: problem size per MPI process (default: nx=ny=nz=10)
-P <px> <py> <pz>: processor topology (default: px=py=pz=1)
-print : prints the system
-printstats : prints preconditioning and convergence stats
-printallstats : prints preconditioning and convergence stats
including residual norms for each iteration
All arguments are optional. A very important option for AMG2023 is the ‘-P’ option. It specifies the MPI process topology on which to run, requiring a total of <Px>*<Py>*<Pz> MPI processes.
The ‘-n’ option allows one to specify the local problem size per MPI process, leading to a global problem size of <Px>*<nx> x <Py>*<ny> x <Pz>*<nz>.
3.6. Validation
The validation criteria for AMG2023 is defined as the convergence criteria for the benchmark.
3.7. Example Scalability Results
To measure strong scalability, it is important to change the size per process with the process topology:
The following results were achieved on RZTopaz for a 3D 7-pt Laplace problem on a 300 x 300 x 300 grid.
srun -n <P*Q*R> amg -P <P> <Q> <R> -n <nx> <ny> <nz> -problem 2
P x Q x R |
nx x ny x nz |
setup time |
solve time |
1 x 1 x 1 |
300x300x300 |
43.37 |
61.85 |
2 x 1 x 1 |
150x300x300 |
31.06 |
42.09 |
2 x 2 x 1 |
150x150x300 |
15.68 |
22.74 |
2 x 2 x 2 |
150x150x150 |
8.44 |
12.59 |
4 x 2 x 2 |
75x150x150 |
5.37 |
8.39 |
4 x 4 x 2 |
75x 75x150 |
2.70 |
6.80 |
P x Q x R |
nx x ny x nz |
setup time |
solve time |
1 x 1 x 1 |
300x300x300 |
17.56 |
20.81 |
2 x 1 x 1 |
150x300x300 |
12.04 |
14.48 |
2 x 2 x 1 |
150x150x300 |
6.35 |
8.78 |
2 x 2 x 2 |
150x150x150 |
3.14 |
6.84 |
4 x 2 x 2 |
75x150x150 |
2.44 |
6.73 |
3.8. Memory Usage
AMG2023’s memory needs are somewhat complicated to describe. They are very dependent on the type of problem solved and the options used. When turning on the ‘-printstats’ option, memory complexities <mc> are displayed, which are defined by the sum of non-zeroes of all matrices (both system matrices and interpolation matrices on all levels) divided by the number of non-zeroes of the original matrix, i.e., at least about <mc> times as much space is needed. However, this does not include memory needed for communication, vectors, auxiliary computations, etc.
The figure below provides information about approximate memory usage on 1 NVIDIA V-100 for Problem 1 (AMG-GMRES, 27pt stencil) and Problem 2 (AMG-PCG, 7pt stencil, with 1 level aggressive coarsening) for increasing problem sizes n x n x n, starting at 0.24 GB for each problem. The black dashed line indicates the GPU memory available on 1 GPU (V-100) on Lassen.
The second figure provides memory use on 1 node of CTS-1 (Quartz) using 4 MPI tasks with 9 OpenMP threads each for Problem 1 and Problem 2 for increasing problem size n x n x n per MPI task.
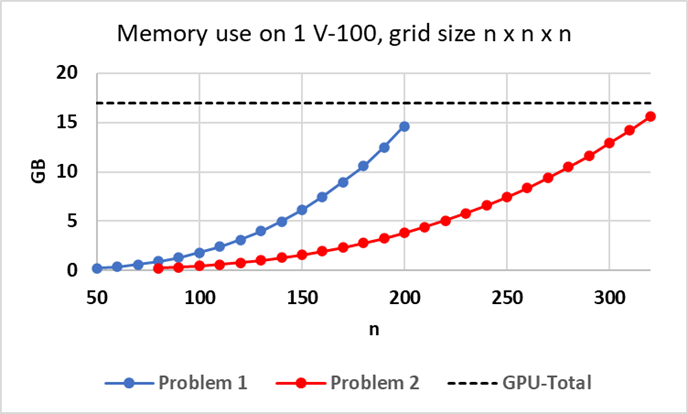
Fig. 3.1 Approximate memory use for Problems 1 and 2 on V-100
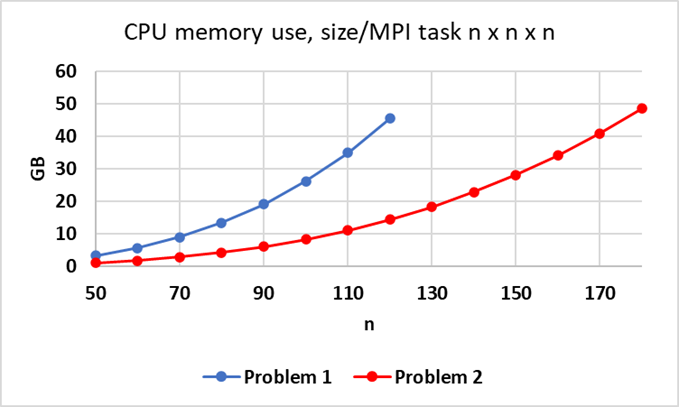
Fig. 3.2 Approximate memory use for Problems 1 and 2 on CTS-1
3.9. Strong Scaling on Crossroads
We present strong scaling results for varying problem sizes on Crossroads with HBM below. The code was configured and compiled using hypre v2.29.0 with MPI only and optimization -O2.
Strong scaling results of AMG2023 for problem 1 on a grid size of 120 x 120 x 120 are provided in the following table and figure.
No. cores |
Actual |
Ideal |
|---|---|---|
1 |
1.2053E+07 |
1.2053E+07 |
2 |
2.3748E+07 |
2.4106E+07 |
4 |
4.4537E+07 |
4.8212E+07 |
8 |
8.1841E+07 |
9.6424E+07 |
16 |
1.5018E+08 |
1.9285E+08 |
32 |
2.6169E+08 |
3.8570E+08 |
64 |
4.0990E+08 |
7.7139E+08 |
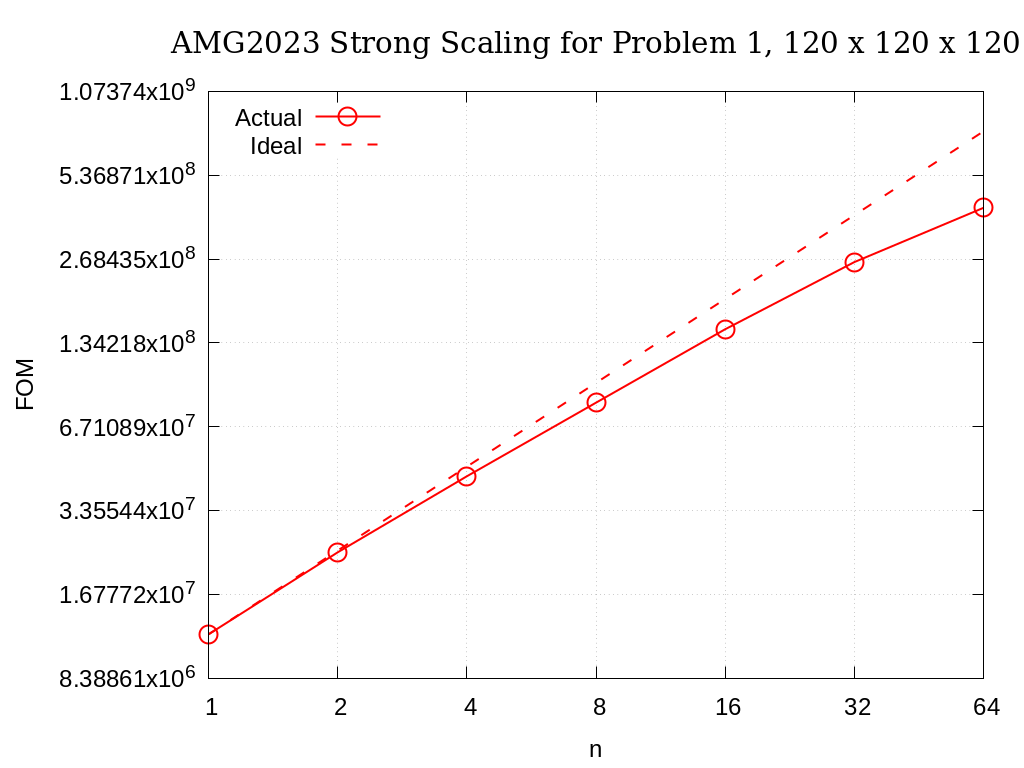
Fig. 3.3 AMG2023 Strong Scaling for Problem 1 (27-pt, AMG-GMRES) on a grid of size 120 x 120 x 120
Strong scaling results of AMG2023 for problem 1 on a grid size of 160 x 160 x 160 are provided in the following table and figure.
No. cores |
Actual |
Ideal |
|---|---|---|
1 |
1.1871E+07 |
1.1871E+07 |
2 |
2.2864E+07 |
2.3743E+07 |
4 |
4.3908E+07 |
4.7486E+07 |
8 |
8.2382E+07 |
9.4972E+07 |
16 |
1.5050E+08 |
1.8994E+08 |
32 |
2.7485E+08 |
3.7989E+08 |
64 |
4.7192E+08 |
7.5977E+08 |
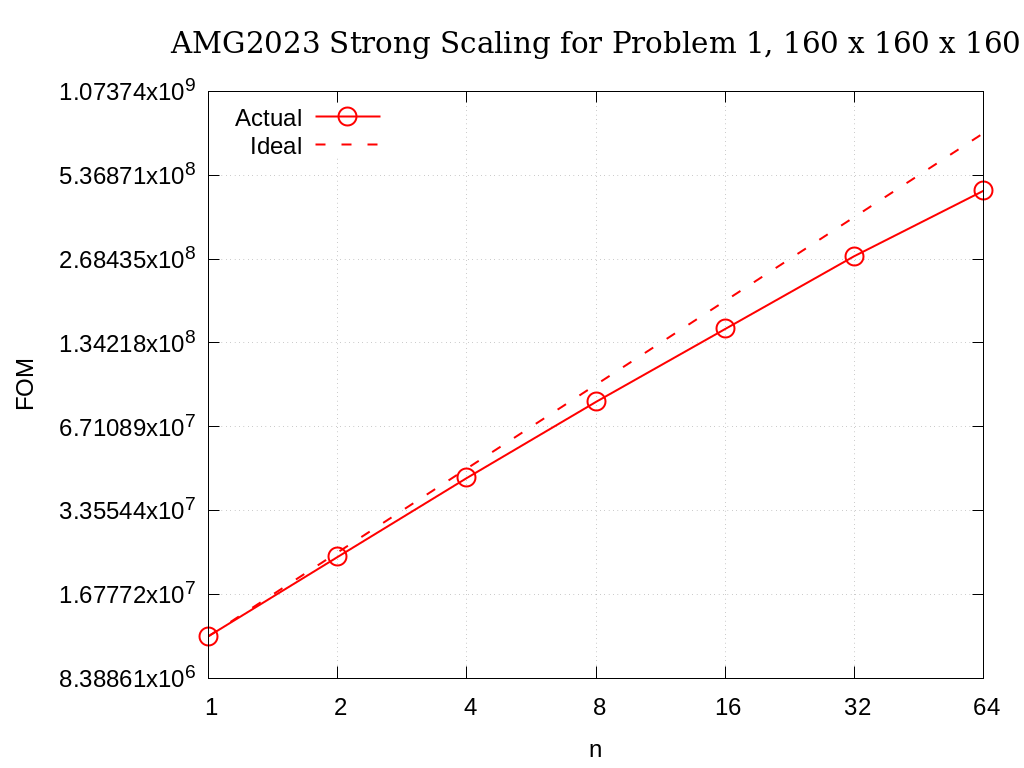
Fig. 3.4 AMG2023 Strong Scaling for Problem 1 (27-pt, AMG-GMRES) on a grid of size 160 x 160 x 160
Strong scaling results of AMG2023 for problem 1 on a grid size of 200 x 200 x 200 are provided in the following table and figure.
No. cores |
Actual |
Ideal |
|---|---|---|
1 |
1.1677E+07 |
1.1677E+07 |
2 |
2.2162E+07 |
2.3354E+07 |
4 |
4.2170E+07 |
4.6708E+07 |
8 |
8.3668E+07 |
9.3415E+07 |
16 |
1.4897E+08 |
1.8683E+08 |
32 |
2.7608E+08 |
3.7366E+08 |
64 |
5.0217E+08 |
7.4732E+08 |
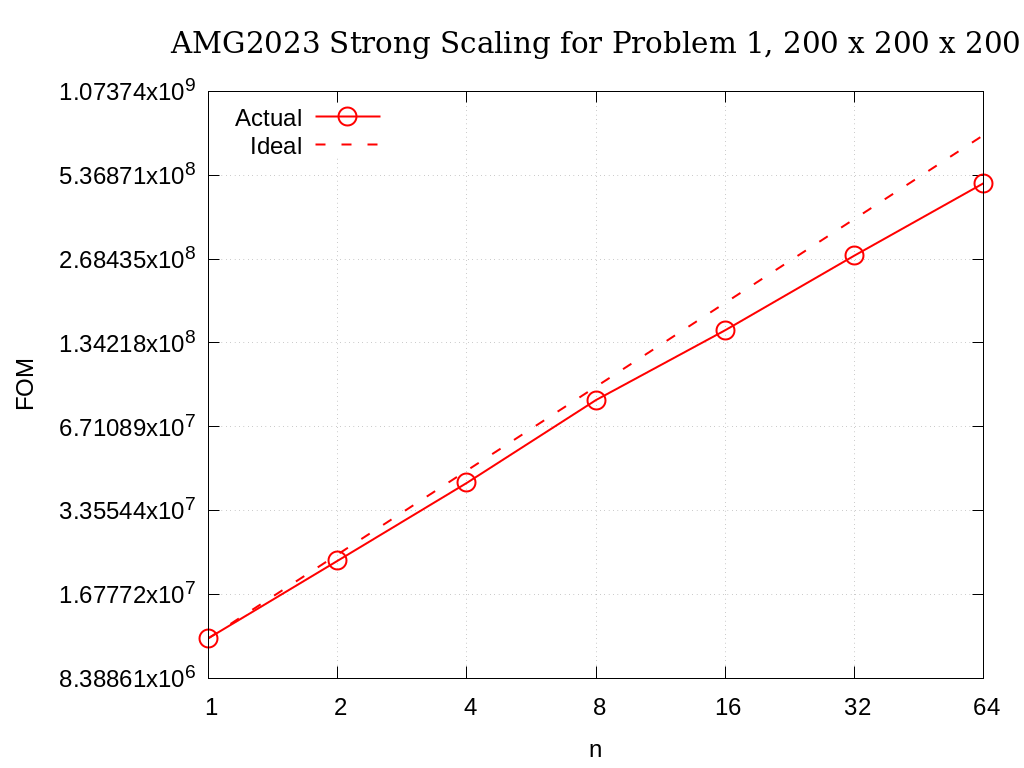
Fig. 3.5 AMG2023 Strong Scaling for Problem 1 (27-pt, AMG-GMRES) on a grid of size 200 x 200 x 200
Strong scaling results of AMG2023 for problem 2 on a grid size of 200 x 200 x 200 are provided in the following table and figure.
No. cores |
Actual |
Ideal |
|---|---|---|
1 |
2.7956E+06 |
2.7956E+06 |
2 |
5.0762E+06 |
5.5913E+06 |
4 |
9.3707E+06 |
1.1183E+07 |
8 |
1.7585E+07 |
2.2365E+07 |
16 |
3.2401E+07 |
4.4730E+07 |
32 |
5.8306E+07 |
8.9460E+07 |
64 |
1.0401E+08 |
1.7892E+08 |
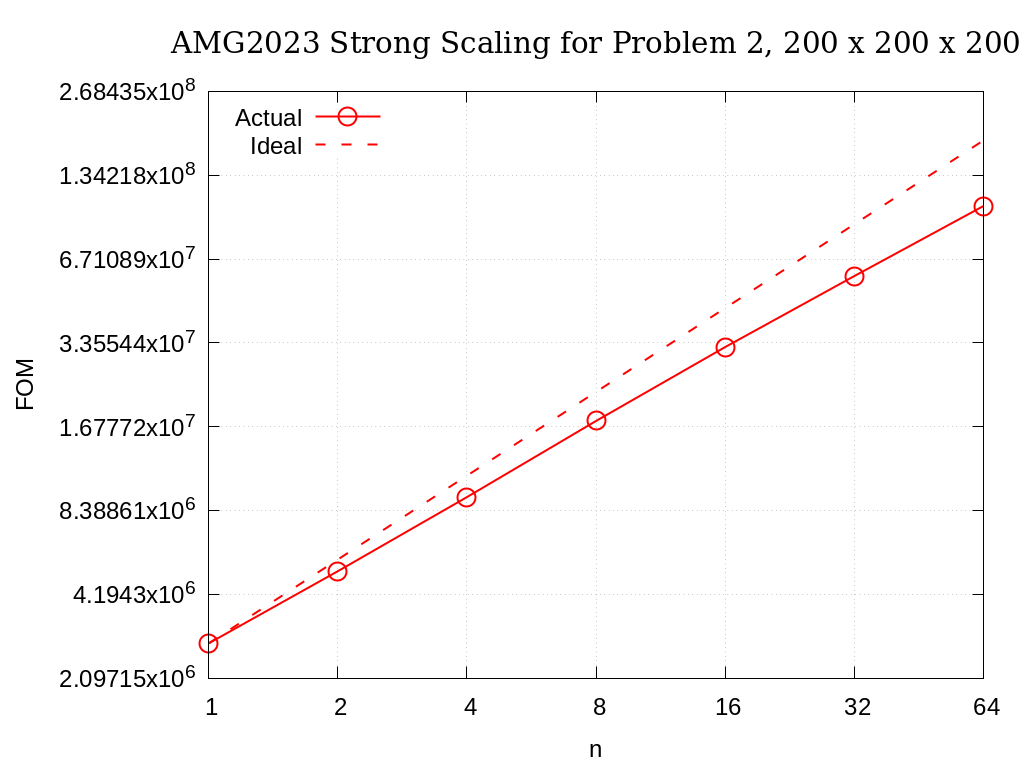
Fig. 3.6 AMG2023 Strong Scaling for Problem 2 (7-pt, AMG-PCG) on a grid of size 200 x 200 x 200
Strong scaling results of AMG2023 for problem 2 on a grid size of 256 x 256 x 256 are provided in the following table and figure.
No. cores |
Actual |
Ideal |
|---|---|---|
1 |
2.5400E+06 |
2.5400E+06 |
2 |
4.6956E+06 |
5.0801E+06 |
4 |
8.5277E+06 |
1.0160E+07 |
8 |
1.6098E+07 |
2.0320E+07 |
16 |
2.9559E+07 |
4.0640E+07 |
32 |
5.5629E+07 |
8.1281E+07 |
64 |
1.0656E+08 |
1.6256E+08 |
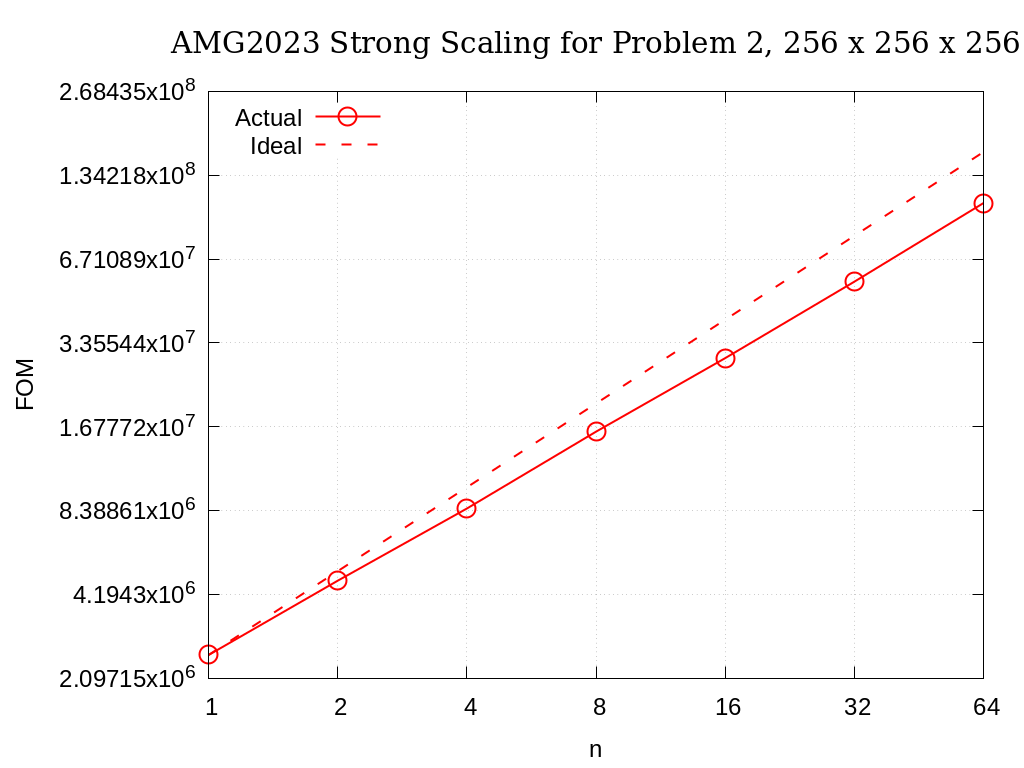
Fig. 3.7 AMG2023 Strong Scaling for Problem 2 (7-pt, AMG-PCG) on a grid of size 256 x 256 x 256
Strong scaling results of AMG2023 for problem 2 on a grid size of 320 x 320 x 320 are provided in the following table and figure.
No. cores |
Actual |
Ideal |
|---|---|---|
1 |
2.3462E+06 |
2.3462E+06 |
2 |
4.2833E+06 |
4.6925E+06 |
4 |
7.8280E+06 |
9.3849E+06 |
8 |
1.5619E+07 |
1.8770E+07 |
16 |
2.8615E+07 |
3.7540E+07 |
32 |
5.2880E+07 |
7.5079E+07 |
64 |
9.5875E+07 |
1.5016E+08 |
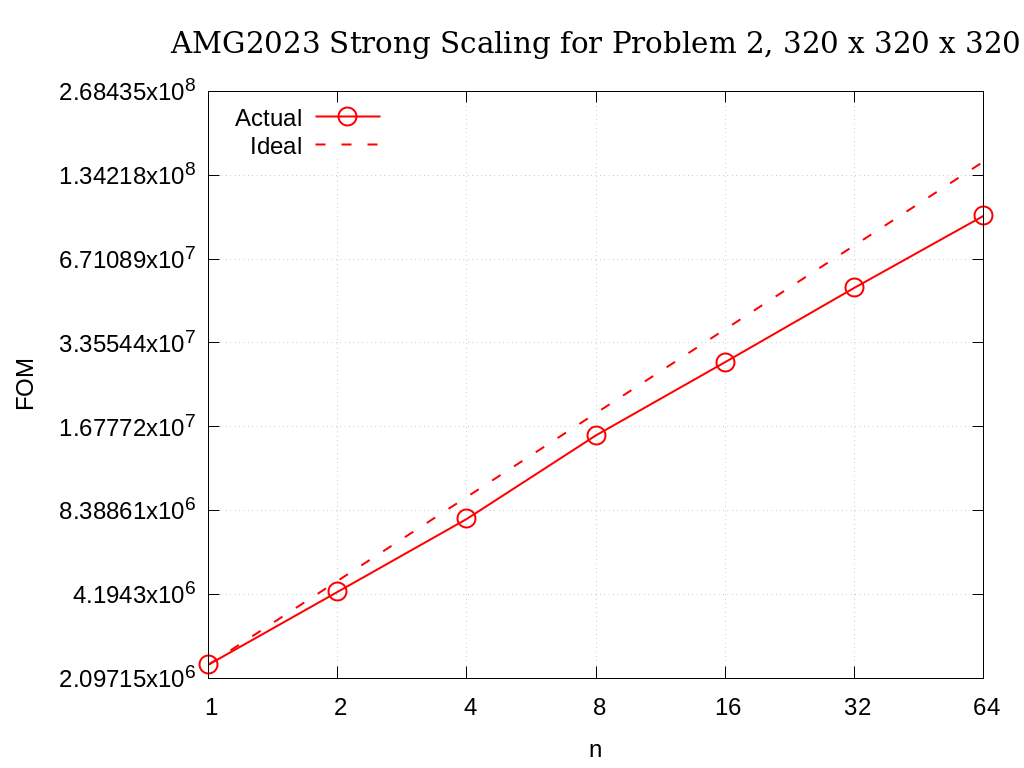
Fig. 3.8 AMG2023 Strong Scaling for Problem 2 (7-pt, AMG-PCG) on a grid of size 320 x 320 x 320
Approximate results of the FOM for varying memory usages on Crossroads are provided in the following table and figure. Note that the actual size in GB is only an estimate.
GB |
Problem 1 |
Problem 2 |
|---|---|---|
10 |
1.2197E+07 |
2.8391E+06 |
20 |
1.2055E+07 |
2.7853E+06 |
30 |
1.1929E+07 |
2.6162E+06 |
40 |
1.1904E+07 |
2.5890E+06 |
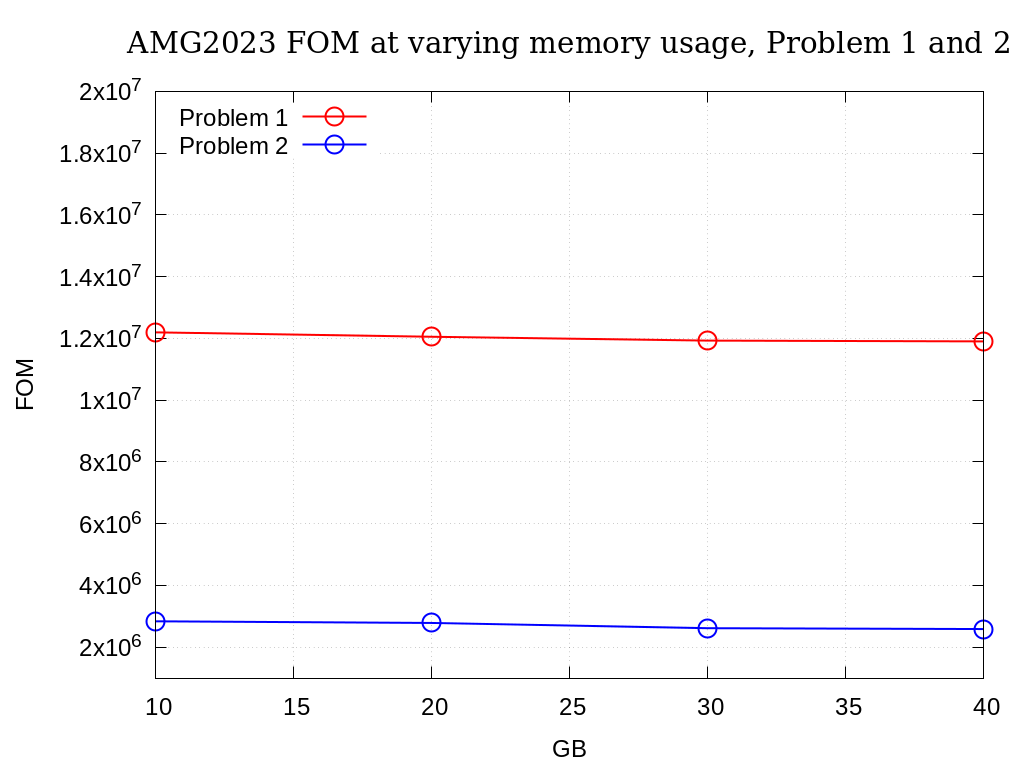
Fig. 3.9 Varying memory usage (estimated) for Problem 1 and 2
3.10. V-100
We have also performed runs on 1 NVIDIA V-100 GPU increasing the problem size n x n x n. For these runs hypre 2.29.0 was configured as follows:
configure --with-cuda
We increased n by 10 starting with n=50 for Problem 1 and with n=80 for Problem 2 until we ran out of memory. Note that Problem 2 uses much less memory, since the original matrix has at most 7 coefficients per row vs 27 for Problem 1. In addition, aggressive coarsening is used on the first level, significantly decreasing memory usage at the cost of increased number of iterations.
The FOMs of AMG2023 on V100 for Problem 1 is provided in the following table and figure:
n |
FOM |
|---|---|
50 |
7.135E+07 |
60 |
9.863E+07 |
70 |
1.199E+08 |
80 |
1.397E+08 |
90 |
1.629E+08 |
100 |
1.858E+08 |
110 |
2.104E+08 |
120 |
2.317E+08 |
130 |
2.496E+08 |
140 |
2.597E+08 |
150 |
2.668E+08 |
160 |
2.733E+08 |
170 |
2.827E+08 |
180 |
2.858E+08 |
190 |
2.890E+08 |
200 |
2.925E+08 |
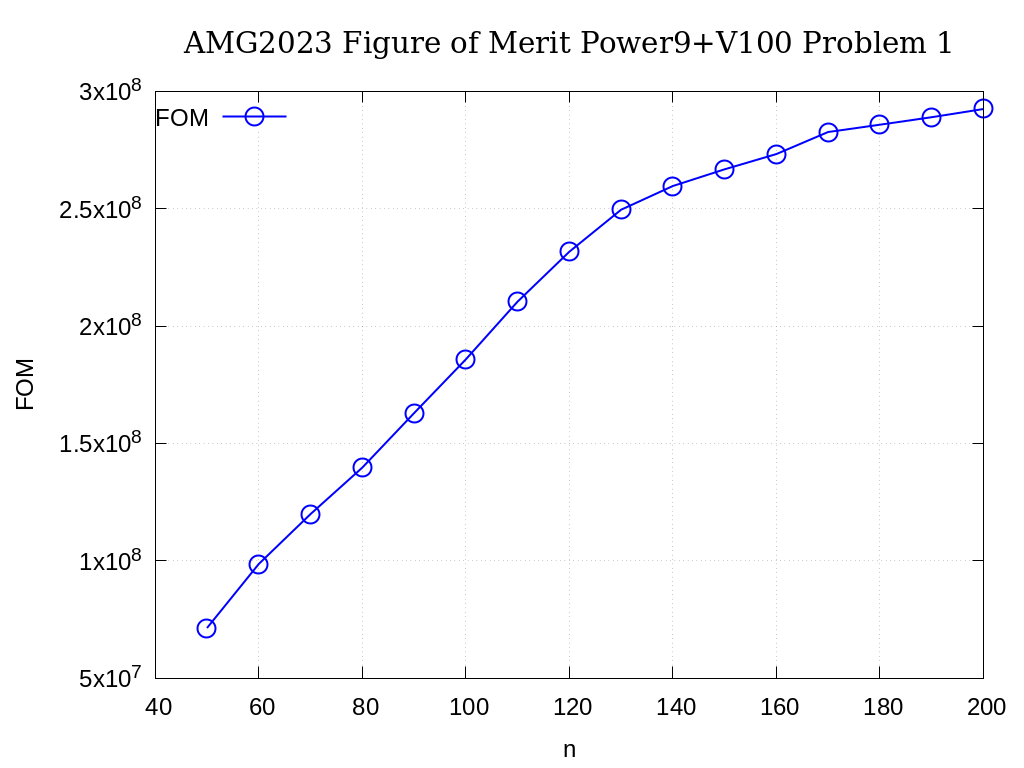
Fig. 3.10 AMG2023 FOM on V100 for Problem 1 (27-pt stencil, AMG-GMRES)
The FOMs of AMG2023 on V100 for Problem 2 is provided in the following table and figure:
n |
FOM |
|---|---|
80 |
2.931E+07 |
90 |
3.493E+07 |
100 |
4.070E+07 |
110 |
4.437E+07 |
120 |
4.511E+07 |
130 |
5.104E+07 |
140 |
5.510E+07 |
150 |
5.842E+07 |
160 |
6.075E+07 |
170 |
6.276E+07 |
180 |
6.530E+07 |
190 |
6.652E+07 |
200 |
6.823E+07 |
210 |
6.903E+07 |
220 |
6.949E+07 |
230 |
6.821E+07 |
240 |
6.856E+07 |
250 |
6.871E+07 |
260 |
6.910E+07 |
270 |
6.801E+07 |
280 |
6.825E+07 |
290 |
6.916E+07 |
300 |
6.932E+07 |
310 |
6.955E+07 |
320 |
6.978E+07 |
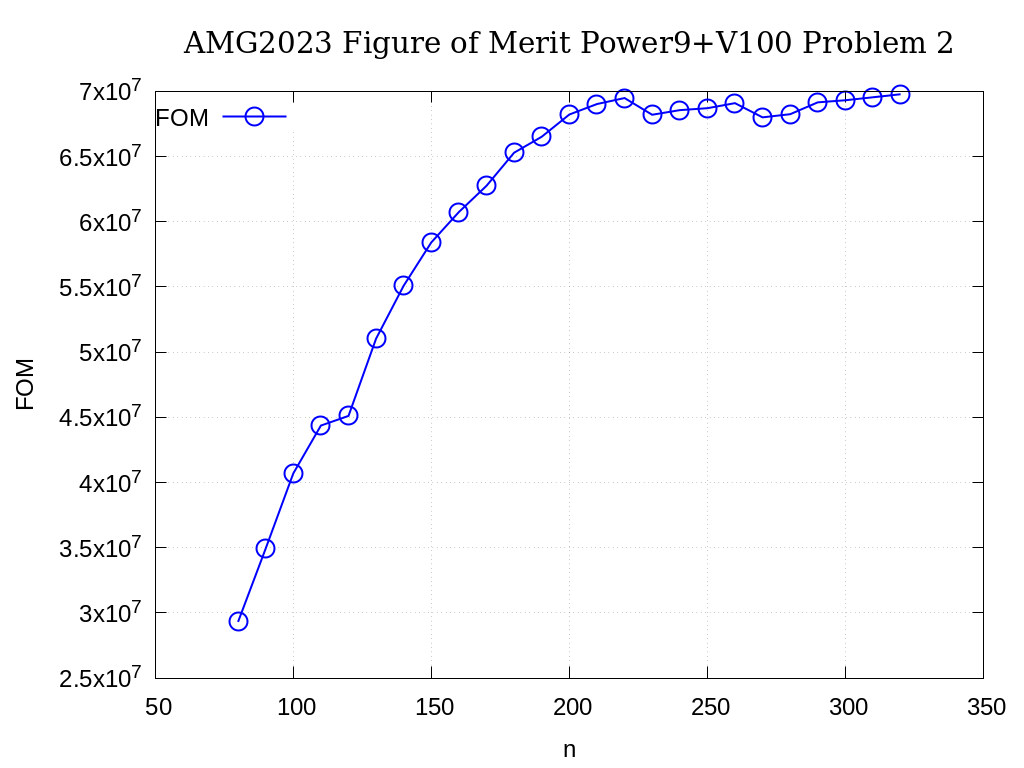
Fig. 3.11 AMG2023 FOM on V100 for Problem 2 (7-pt stencil, AMG-PCG)
3.11. Multi-node scaling on Crossroads
The results of the scaling runs performed on Crossroadsare presented below.
Amg and hypre were built with intel oneapi 2023.1.0 and cray-mpich 8.1.25.
These runs used 32 to 2048 nodes with 108 tasks per node.
Problems 1 and 2 were run with problem sizes per MPI process, -n, of 38,38,38 and 60,60,60 respectively to use roughly 15% of available memory while maintaining a cubic grid.
The product of the x,y,z process topology must equal the number of processors.
In this case, x=y=24 for all node counts and z was set to 6, 12, and 18 for 32, 64, and 96 nodes respectively.
Output files can be found in ./docs/sphinx/02_amg/scaling/output/
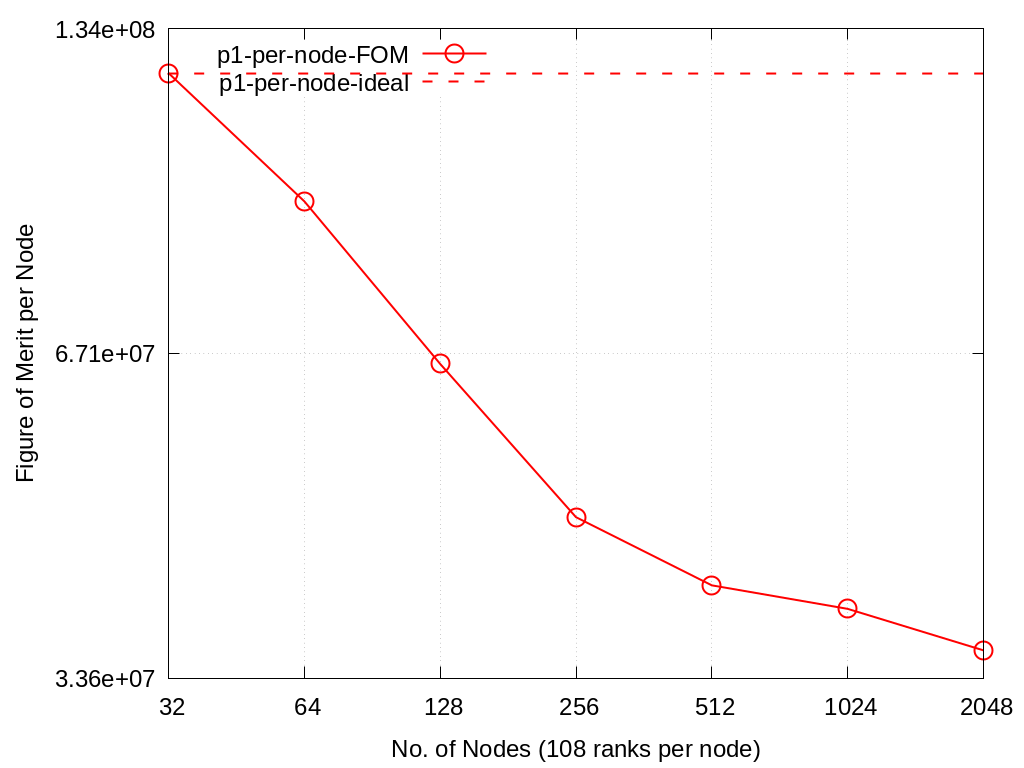
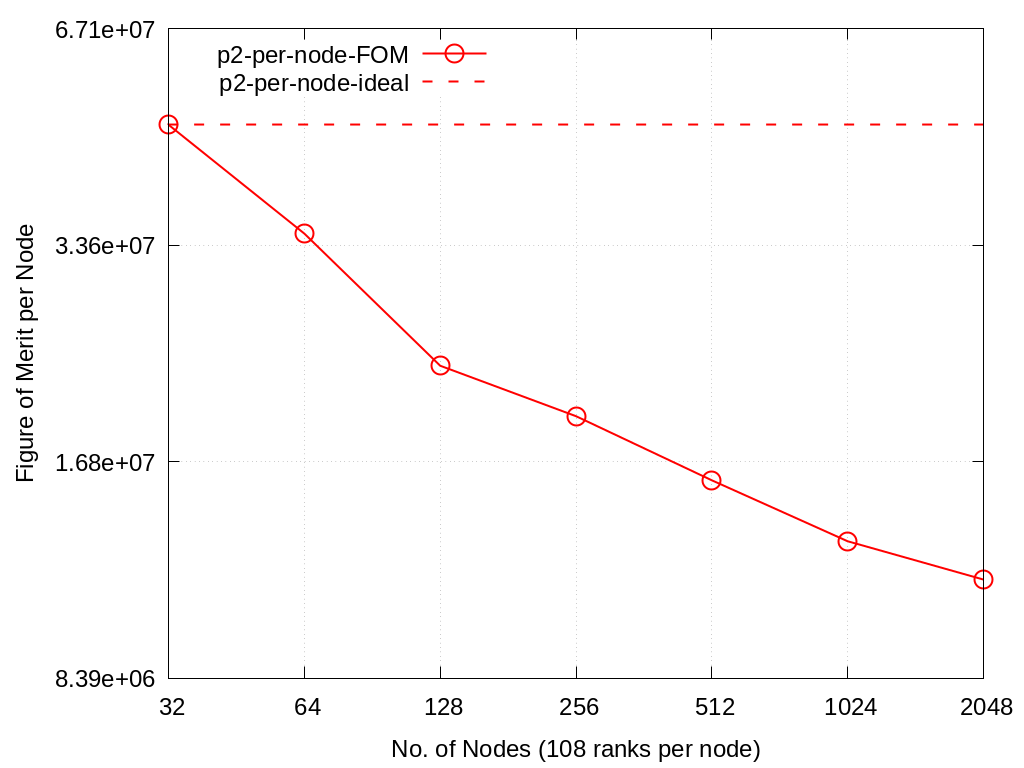
Nodes |
Problem1 |
Problem2 |
p1-per-node-FOM |
p2-per-node-FOM |
p1-per-node-ideal |
p2-per-node-ideal |
|---|---|---|---|---|---|---|
32 |
3.90E+09 |
1.58E+09 |
1.22E+08 |
4.93E+07 |
1.22E+08 |
4.93E+07 |
64 |
5.94E+09 |
2.23E+09 |
9.28E+07 |
3.48E+07 |
1.22E+08 |
4.93E+07 |
128 |
8.39E+09 |
2.92E+09 |
6.56E+07 |
2.28E+07 |
1.22E+08 |
4.93E+07 |
256 |
1.21E+10 |
4.98E+09 |
4.73E+07 |
1.94E+07 |
1.22E+08 |
4.93E+07 |
512 |
2.10E+10 |
8.06E+09 |
4.09E+07 |
1.58E+07 |
1.22E+08 |
4.93E+07 |
1024 |
3.98E+10 |
1.33E+10 |
3.89E+07 |
1.30E+07 |
1.22E+08 |
4.93E+07 |
2048 |
7.29E+10 |
2.36E+10 |
3.56E+07 |
1.15E+07 |
1.22E+08 |
4.93E+07 |
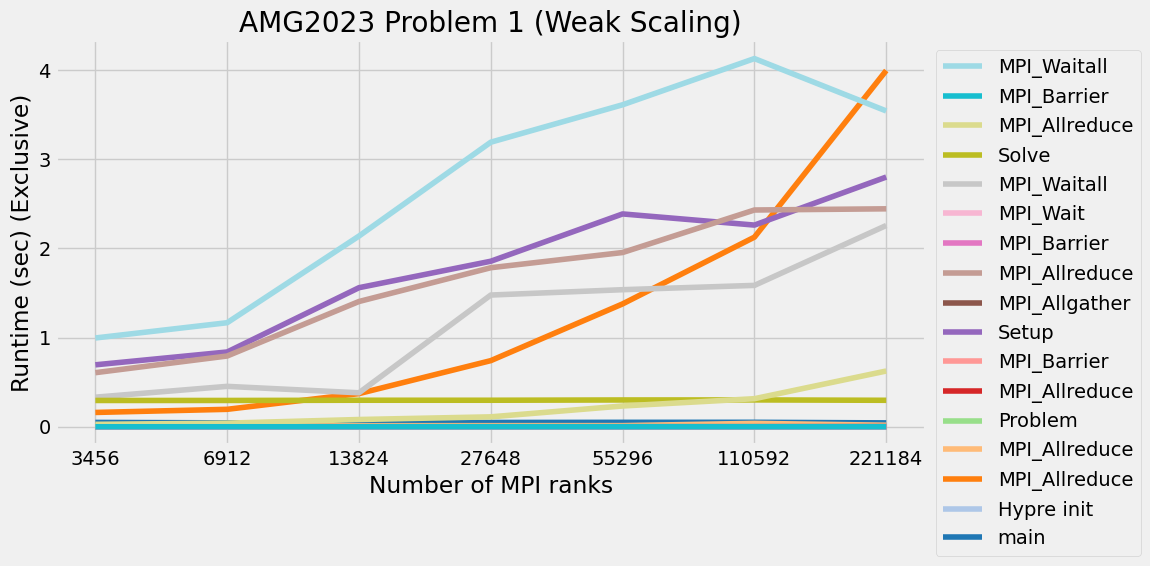
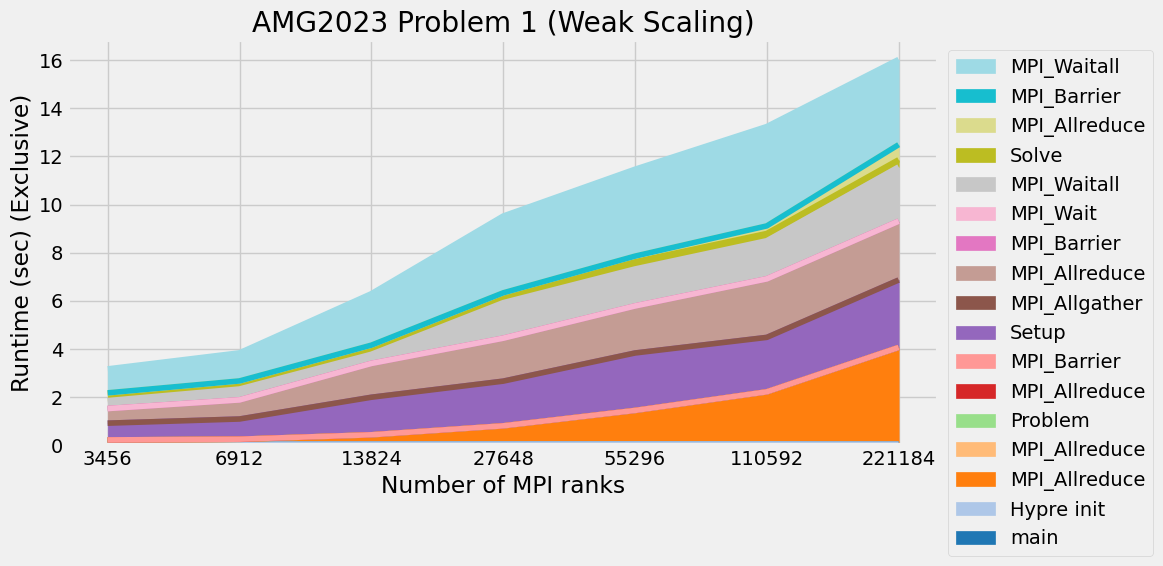
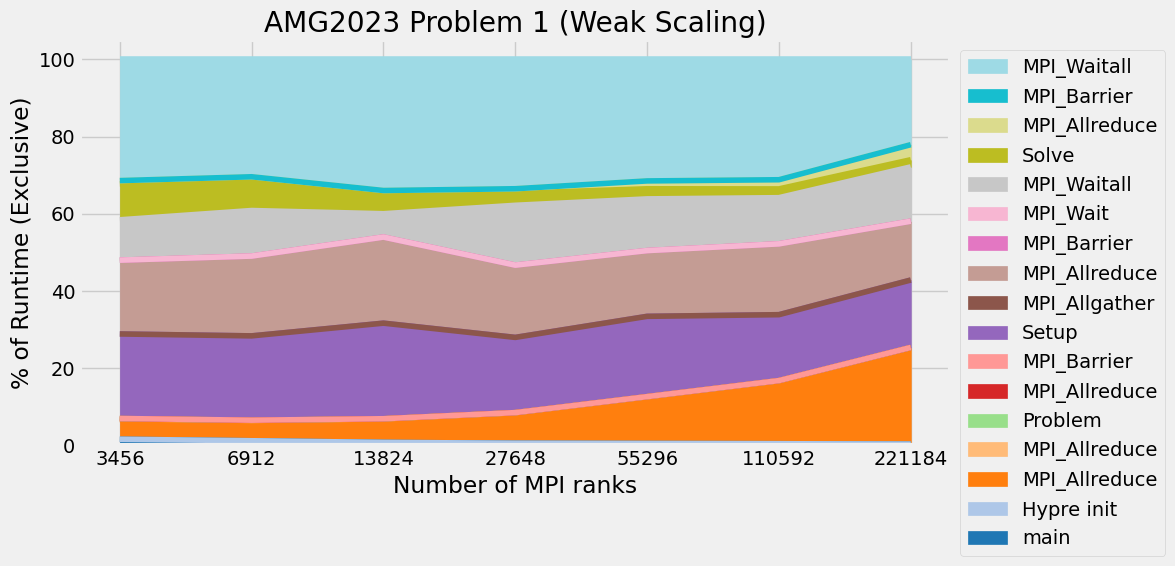
Timings were captured using Caliper and are presented below.
Caliper files can be found in ./doc/sphinx/02_amg/scaling/plots/Caliper
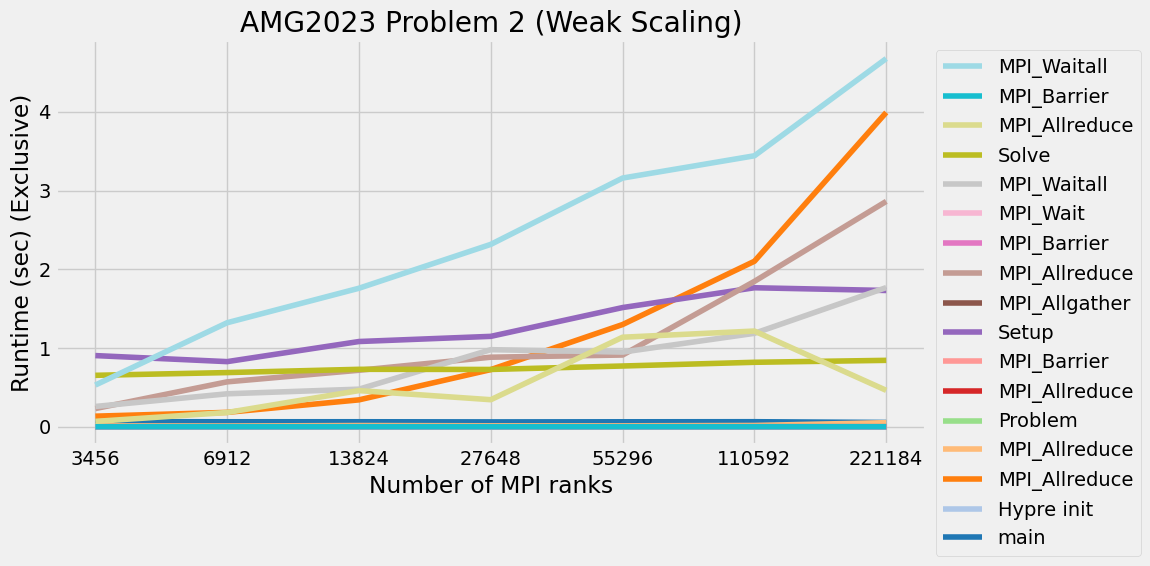
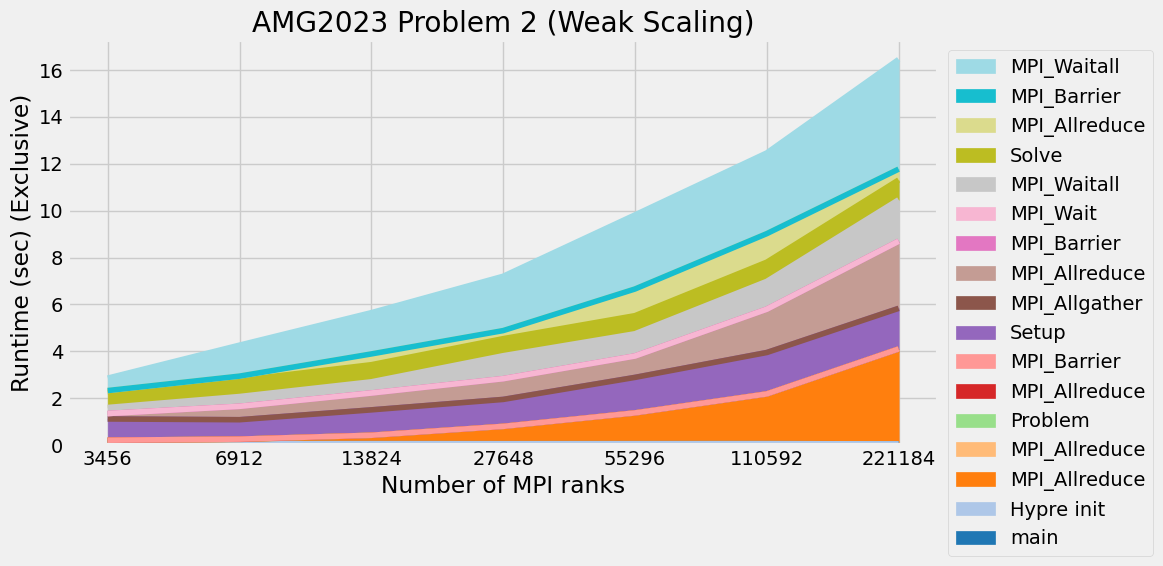
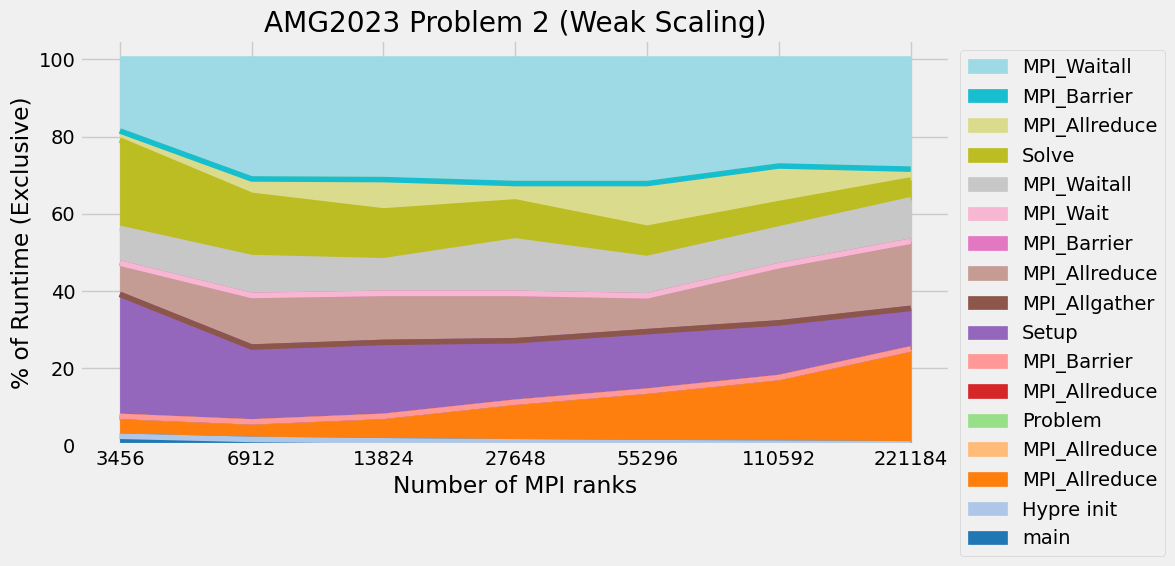
3.12. References
All references are available at https://github.com/hypre-space/hypre/wiki/Publications :
Van Emden Henson and Ulrike Meier Yang, “BoomerAMG: A Parallel Algebraic Multigrid Solver and Preconditioner”, Appl. Num. Math. 41 (2002), pp. 155-177.
Hans De Sterck, Ulrike Meier Yang and Jeffrey Heys, “Reducing Complexity in Parallel Algebraic Multigrid Preconditioners”, SIAM Journal on Matrix Analysis and Applications 27 (2006), pp. 1019-1039.
Hans De Sterck, Robert D. Falgout, Josh W. Nolting and Ulrike Meier Yang, “Distance-Two Interpolation for Parallel Algebraic Multigrid”, Numerical Linear Algebra with Applications 15 (2008), pp. 115-139.
Ulrike Meier Yang, “On Long Range Interpolation Operators for Aggressive Coarsening”, Numer. Linear Algebra Appl., 17 (2010), pp. 453-472.
Allison Baker, Rob Falgout, Tzanio Kolev, and Ulrike Yang, “Multigrid Smoothers for Ultraparallel Computing”, SIAM J. Sci. Comput., 33 (2011), pp. 2864-2887.
Rui Peng Li, Bjorn Sjogreen, Ulrike Yang, “A New Class of AMG Interpolation Methods Based on Matrix-Matrix Multiplications”, SIAM Journal on Scientific Computing, 43 (2021), pp. S540-S564, https://doi.org/10.1137/20M134931X
Rob Falgout, Rui Peng Li, Bjorn Sjogreen, Lu Wang, Ulrike Yang, “Porting hypre to Heterogeneous Computer Architectures: Strategies and Experiences”, Parallel Computing, 108, (2021), a. 102840