Micromorphic Filter

Note

The purpose of this section is to describe the theory and implementation of the Micromorphic Filter, however, this effort is a work-in-progress and otherwise incomplete.

As described in sections Homogenization via Micromorphic Filter and Micromorphic Filter, the Micromorphic Filter calculates stress and deformation measures (see equations (1) and (2)) from DNS data over one or more macroscopic filter domains (\(\mathcal{G}\)) which contain one or more micro-averaging domains (\(\mathcal{G}^\beta\)), where \(\beta\) is the index corresponding to the number and ID of the micro-averaging domains. The following figure depicts a single filter domain with a single micro-averaging domain highlighted for a collection of micro- (or DNS) points, where \(\alpha\) is an index corresponding to the number and ID of the micro-points.

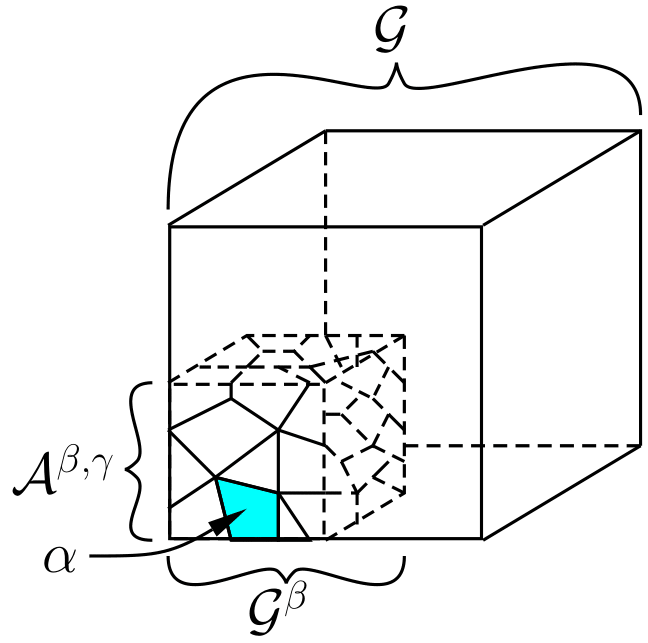
Fig. 43 Micromorphic Filter \(\mathcal{G}\) showing the macroscale volume associated with the \(\beta\text{th}\) Gauss domain (\(\mathcal{G}^\beta\)) and micro-scale point \(\alpha\).

The Micromorphic Filter first determines the macro-scale kinematic quantities for displacements \(\mathbf{u}\) and micro-deformation \(\mathbf{\phi}\) followed by the volume and surface integral quantities defined in Eq. (1). The Micromorphic Filter does not actually calculate the macroscale deformation gradient \(\mathbf{F}\), the micro-deformation tensor \(\mathbf{\chi}\) or the other deformation measures in equation (2), however, it does provide the terms necessary to calculate these quantities including \(u_i\), \(\frac{\partial u_i}{\partial X_I}\), \(\phi_{iI}\), and \(\frac{\partial \phi_{iI}}{\partial X_J}\). Refer to model_package.xdmf_reader_tools.compute_deformations to see how quantities in equation (2) are calculated from the Micromorphic Filter output.

It should be noted that the micro-deformation tensor may be related to a micro-displacement tensor \(\mathbf{\phi}\) as \(\mathbf{\chi} = \mathbf{1} + \mathbf{\phi}\). However, as pointed out by Isbuga 2011 [15], this micro-displacement tensor only exists as a numerical means to interpolate and solve for nine additional dofs that are used to calculate \(\mathbf{\chi}\). Although this is only a small detail within the context of this theory, it is an important for user’s of the Micromorphic Filter.

Note that more than 1 micro-averaging domain is needed to properly determine the relevant deformations.